Here is solutions for Permutations.

1. Understand the problem

• Given an array nums of distinct integers, return all possible permutations. You can return the answer in any order.

• A permutation is a reordering of all elements. For n elements → total permutations = n!

2. Clarify constraints, asks 4 - 5 questions including edge cases.

1. Are all numbers distinct?

• Standard version: ✅ Yes

1. Maximum size of nums?

• Usually 1 ≤ n ≤ 6 or n ≤ 10

• Important because n! grows very fast.

1. Output order matters?

• No, any order is accepted.

1. Should we return a list or print?

• Return a list of lists.

1. Edge cases?

• nums = [] → usually return [[]]

• nums = [1] → [[1]]

3. Explore examples.

1. Example 1

Input: [1,2,3]
Output:
[
 [1,2,3],
 [1,3,2],
 [2,1,3],
 [2,3,1],
 [3,1,2],
 [3,2,1]
]

1. Example 2

Input: [0,1]
Output: [[0,1], [1,0]]

1. Example 3

Input: [1]
Output: [[1]]

4. Brainstorm 2 - 3 solutions, naive solution first and optimize later. Explain the key idea of each solution.

4.1. Solution 1 — Naive Backtracking with Used Array - Time O(N * N!), Space O(N)

• Idea: Build an array and swap in another position.

  • Build permutations one number at a time.

  • Use a used[] array to avoid reusing elements.

  • Try every unused number at each position.

• Time: O(N * N!)

• Space: O(N) recursion + result storage

4.2. In-Place Swapping (Optimized Space)

• Idea:

  • Fix one index at a time.

  • Swap current index with every possible index.

  • Generate permutations without extra space for used[].

• Time: O(N * N!).

• Space: O(1)

5. Implement solutions.

5.1. Recursion - Time O(N * N!), Space O(N * N!)

• Idea:

perms = self.permute(nums[1:])

=> Give me all permutations of the array without the first element.

• Then:

for p in perms:
    for i in range(len(p) + 1):
        insert nums[0] into position i of p

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        if len(nums) == 0:
            return [[]]

        perms = self.permute(nums[1:])
        res = []
        for p in perms:
            for i in range(len(p) + 1):
                p_copy = p.copy()
                p_copy.insert(i, nums[0])
                res.append(p_copy)
        return res

• Time: O(N * N!)

• Space: O(N * N!)

5.2. Iteration - Time O(N * N!), Space O(N * N!)

• For [], Insert 1:

perms = [[1]]

• For [1], Insert 2:

  • Insert at pos 0 → [2,1]

  • Insert at pos 1 → [1,2]

• Insert 3

  • For [2,1]:

    • [3,2,1]

    • [2,3,1]

    • [2,1,3]

  • For [1,2]:

    • [3,1,2]

    • [1,3,2]

    • [1,2,3]

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        perms = [[]]
        for num in nums:
            new_perms = []
            for p in perms:
                for i in range(len(p) + 1):
                    p_copy = p.copy()
                    p_copy.insert(i, num)
                    new_perms.append(p_copy)
            perms = new_perms
        return perms

• Time: O(N * N!)

• Space: O(N * N!)

5.3. Backtracking - Idea like Bit Manipulation - Time O(N * N!), Space O(N * N!)

Idea:

perm = [1]
pick = [T, F, F]

perm = [1, 2]
pick = [T, T, F]

perm = [1, 2, 3]
pick = [T, T, T]
→ ✅ Save [1,2,3]

perm = [1,2]
pick = [T, T, F]

perm = [1,3]
pick = [T, F, T]

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        self.res = []
        self.backtrack([], nums, [False] * len(nums))
        return self.res

    def backtrack(self, perm: List[int], nums: List[int], pick: List[bool]):
        if len(perm) == len(nums):
            self.res.append(perm[:])
            return
        for i in range(len(nums)):
            if not pick[i]:
                perm.append(nums[i])
                pick[i] = True
                self.backtrack(perm, nums, pick)
                perm.pop()
                pick[i] = False

• Time: O(N * N!)

• Space: O(N * N!)

5.4. Bit Manipulation - Time O(N * N!), Space O(N * N!)

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        self.res = []
        self.backtrack([], nums, 0)
        return self.res

    def backtrack(self, perm: List[int], nums: List[int], mask: int):
        if len(perm) == len(nums):
            self.res.append(perm[:])
            return
        for i in range(len(nums)):
            if not (mask & (1 << i)):
                perm.append(nums[i])
                self.backtrack(perm, nums, mask | (1 << i))
                perm.pop()

• Time: O(N * N!)

• Space: O(N * N!)

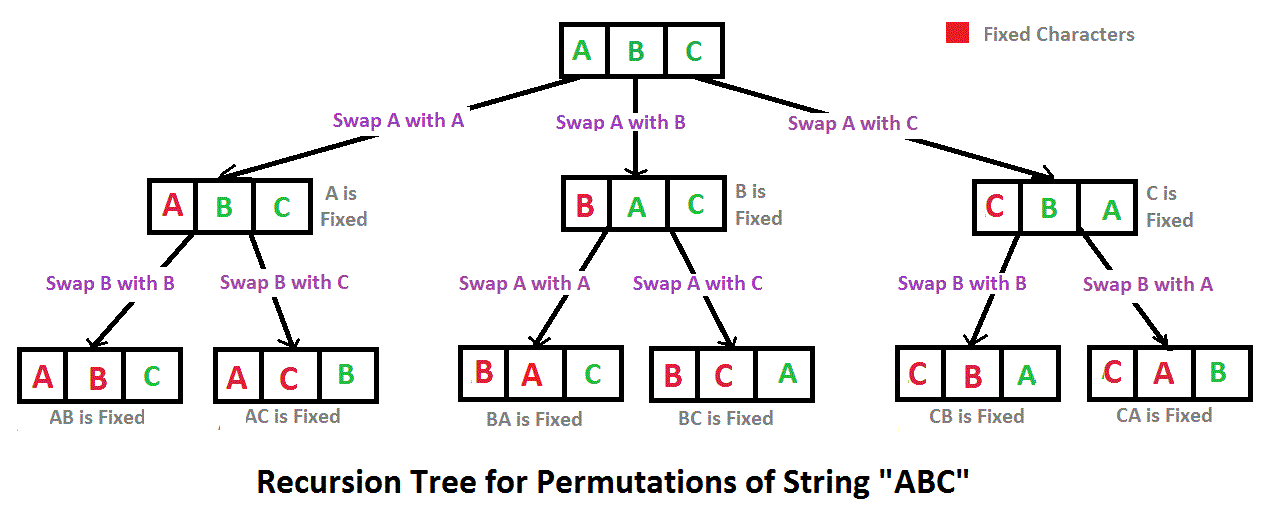
5.5. In-place swapping - Time O(N * N!), Space O(N * N!)

• Idea: Try backtrack when idx = 1

  • idx = the current position we are fixing

  • Positions 0 … idx-1 are already finalized

  • Positions idx … end are candidates to place at idx

• Level 1 → Fix position 1

  • Place 2 at position 1:

  [1, 2, 3]
  
  

  • Place 3 at position 1:

  [1, 3, 2]
  

class Solution:
    def permute(self, nums: List[int]) -> List[List[int]]:
        self.res = []
        self.backtrack(nums, 0)
        return self.res

    def backtrack(self, nums: List[int], idx: int):
        if idx == len(nums):
            self.res.append(nums[:])
            return
        for i in range(idx, len(nums)):
            nums[idx], nums[i] = nums[i], nums[idx]
            self.backtrack(nums, idx + 1)
            nums[idx], nums[i] = nums[i], nums[idx]

• Time: O(N * N!)

• Space: O(N * N!)

6. Dry run testcases.