Framework Thinking - Neetcode 150 - Subsets
Here is solutions for Subsets.
1. Understand the problem
-
Given an integer array nums of unique elements, return all possible subsets (the power set).
-
The solution set must not contain duplicate subsets. You can return the answer in any order.
2. Clarify constraints, asks 4 - 5 questions including edge cases.
- Size of nums?
-
e.g. 1 <= len(nums) <= 10 or maybe up to 20.
-
This matters because the number of subsets is 2^n. If n = 20, that’s 1,048,576 subsets—big but still OK.
- Elements unique?
-
Usually: Yes, all elements are distinct.
-
If no, we would need extra work to avoid duplicate subsets (that’s another problem: “Subsets II”).
- Can elements be negative or zero?
-
Usually: yes, they can be any integers.
-
It doesn’t affect the algorithm, because we only care about positions, not value size.
- Output order requirements?
-
Often: any order is fine.
-
If they want a specific order (e.g. sorted subsets, or lexicographic), we might sort nums first and/or handle output ordering.
- Memory constraints?
-
We must output all subsets, so space complexity at least O(2^n * n) is unavoidable.
-
Ask if that is acceptable (usually: yes).
3. Explore examples.
- Example 1
Input: nums = [1, 2]
Output: [[], [1], [2], [1,2]]
- Example 2
Input: nums = [1, 2, 3]
Output (any order):
[
[],
[1], [2], [3],
[1,2], [1,3], [2,3],
[1,2,3]
]
4. Brainstorm 2 - 3 solutions, naive solution first and optimize later. Explain the key idea of each solution.
4.1. Solution A – Naive Backtracking (DFS, include/exclude) - Time O(2^N * N), Space O(N)
Key idea
-
We explore all choices: for each position i, we have two options:
-
Include nums[i] in the current subset.
-
Exclude nums[i] from the current subset.
-
dfs(i, path):
if i == n:
add copy of path to result
return
# choice 1: skip nums[i]
dfs(i + 1, path)
# choice 2: take nums[i]
path.append(nums[i])
dfs(i + 1, path)
path.pop() # backtrack
-
Time: O(2^N * N) (2^n subsets, each up to size n)
-
Space: O(N).
4.2. Solution B – Iterative “build up subsets” - Time O(2^N * N), Space O(N)
Key idea
- Start with just the empty subset and for each number, clone existing subsets and append the new number.
Start: res = [[]]
- Take 1: new subsets = [ [1] ] → res = [[], [1]]
- Take 2: new subsets = [[2], [1,2]] → res = [[], [1], [2], [1,2]]
- Take 3: new subsets = [[3], [1,3], [2,3], [1,2,3]] and so on.
- Time/Space: same as backtracking, O(2^n * n).
4.3. Solution C – Bitmasking - Time O(2^N * N), Space O(N)
Key idea
-
A set of n elements has 2^n subsets. We can represent each subset using an n-bit number from 0 to 2^n - 1:
-
If the j-th bit of mask is 1, include nums[j] in the subset.
-
Example for nums = [1,2,3]:
-
mask = 0 (binary 000) → []
-
mask = 1 (binary 001) → [1]
-
mask = 2 (binary 010) → [2]
-
mask = 3 (binary 011) → [1,2]
…
-
-
Time: O(2^n * n) (for each mask, scan n bits)
-
Space: O(2^n * n) for output.
5. Implement solutions.
5.1. Backtracking - Time O(N * 2^N), Space O(N)
from typing import List
class SolutionBacktracking:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = []
n = len(nums)
def dfs(i: int, path: List[int]) -> None:
# Base case: we've decided for all positions
if i == n:
# Append a copy of the current subset
res.append(path.copy())
return
# Choice 1: do not include nums[i]
dfs(i + 1, path)
# Choice 2: include nums[i]
path.append(nums[i])
dfs(i + 1, path)
# Backtrack
path.pop()
dfs(0, [])
return res
| Step | Call / Action | i | path (before action) | res |
|---|---|---|---|---|
| 1 | dfs(0, []) start | 0 | [] | [] |
| 2 | dfs(1, []) — exclude 1 | 1 | [] | [] |
| 3 | dfs(2, []) — exclude 2 | 2 | [] | [] |
| 4 | dfs(3, []) — exclude 3 | 3 | [] | append [] → [[]] |
| 5 | return to dfs(2), include 3 | 2 | [] → [3] | |
| 6 | dfs(3, [3]) | 3 | [3] | append [3] → [[], [3]] |
| 7 | backtrack → pop 3 | 2 | [3] → [] | |
| 8 | return to dfs(1), include 2 | 1 | [] → [2] | |
| 9 | dfs(2, [2]) — exclude 3 | 2 | [2] | |
| 10 | dfs(3, [2]) | 3 | [2] | append [2] → [[], [3], [2]] |
| 11 | return to dfs(2), include 3 | 2 | [2] → [2,3] | |
| 12 | dfs(3, [2,3]) | 3 | [2,3] | append [2,3] → [[], [3], [2], [2,3]] |
| 13 | backtrack → pop 3 | 2 | [2,3] → [2] | |
| 14 | backtrack → pop 2 | 1 | [2] → [] | |
| 15 | return to dfs(0), include 1 | 0 | [] → [1] | |
| 16 | dfs(1, [1]) — exclude 2 | 1 | [1] | |
| 17 | dfs(2, [1]) — exclude 3 | 2 | [1] | |
| 18 | dfs(3, [1]) | 3 | [1] | append [1] → [[], [3], [2], [2,3], [1]] |
| 19 | return to dfs(2), include 3 | 2 | [1] → [1,3] | |
| 20 | dfs(3, [1,3]) | 3 | [1,3] | append [1,3] → [[], [3], [2], [2,3], [1], [1,3]] |
| 21 | backtrack → pop 3 | 2 | [1,3] → [1] | |
| 22 | return to dfs(1), include 2 | 1 | [1] → [1,2] | |
| 23 | dfs(2, [1,2]) — exclude 3 | 2 | [1,2] | |
| 24 | dfs(3, [1,2]) | 3 | [1,2] | append [1,2] → [[], [3], [2], [2,3], [1], [1,3], [1,2]] |
| 25 | return to dfs(2), include 3 | 2 | [1,2] → [1,2,3] | |
| 26 | dfs(3, [1,2,3]) | 3 | [1,2,3] | append [1,2,3] → [[], [3], [2], [2,3], [1], [1,3], [1,2], [1,2,3]] |
| 27 | backtrack → pop 3 | 2 | [1,2,3] → [1,2] | |
| 28 | backtrack → pop 2 | 1 | [1,2] → [1] | |
| 29 | backtrack → pop 1 | 0 | [1] → [] | |
| 30 | recursion ends | — | — | ✅ final result |
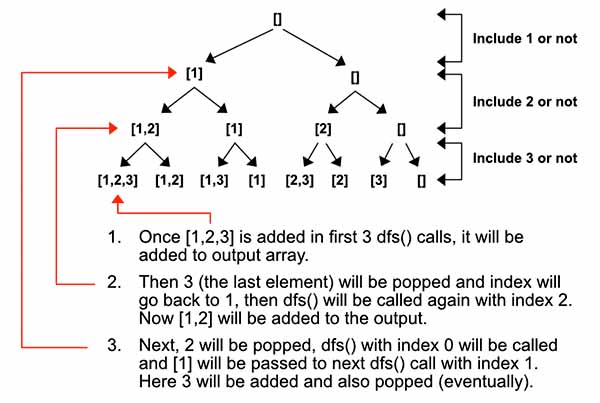
Notes: In [1, 3] => 1 in the under loop, 3 in the above loop.
-
Time: O(N * 2^N).
-
Space: O(N) extra space
5.2. Iteration - Time O(N * 2^N), Space O(N)
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
res = [[]]
for num in nums:
res += [subset + [num] for subset in res]
return res
-
Time: O(N * 2^N).
-
Space: O(N) extra space
| num | res (before) | new subsets | res (after) |
|---|---|---|---|
| 1 | [[]] |
[[1]] |
[[], [1]] |
| num | res (before) | new subsets | res (after) |
|---|---|---|---|
| 2 | [[], [1]] |
[[2], [1,2]] |
[[], [1], [2], [1,2]] |
| num | res (before) | new subsets | res (after) |
|---|---|---|---|
| 3 | [[], [1], [2], [1,2]] |
[[3], [1,3], [2,3], [1,2,3]] |
[[], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3]] |
5.3. Bit Manipulation - Time O(N * 2^N), Space O(N)
class Solution:
def subsets(self, nums: List[int]) -> List[List[int]]:
n = len(nums)
res = []
for i in range(1 << n):
subset = [nums[j] for j in range(n) if (i & (1 << j))]
res.append(subset)
return res
-
Time: O(N * 2^N).
-
Space: O(N) extra space
6. Dry run testcases.
Example: [1,2,3]
- Solution 1:
| Step | Call / Action | i | path (before action) | res |
|---|---|---|---|---|
| 1 | dfs(0, []) start | 0 | [] | [] |
| 2 | dfs(1, []) — exclude 1 | 1 | [] | [] |
| 3 | dfs(2, []) — exclude 2 | 2 | [] | [] |
| 4 | dfs(3, []) — exclude 3 | 3 | [] | append [] → [[]] |
| 5 | return to dfs(2), include 3 | 2 | [] → [3] | |
| 6 | dfs(3, [3]) | 3 | [3] | append [3] → [[], [3]] |
| 7 | backtrack → pop 3 | 2 | [3] → [] | |
| 8 | return to dfs(1), include 2 | 1 | [] → [2] | |
| 9 | dfs(2, [2]) — exclude 3 | 2 | [2] | |
| 10 | dfs(3, [2]) | 3 | [2] | append [2] → [[], [3], [2]] |
| 11 | return to dfs(2), include 3 | 2 | [2] → [2,3] | |
| 12 | dfs(3, [2,3]) | 3 | [2,3] | append [2,3] → [[], [3], [2], [2,3]] |
| 13 | backtrack → pop 3 | 2 | [2,3] → [2] | |
| 14 | backtrack → pop 2 | 1 | [2] → [] | |
| 15 | return to dfs(0), include 1 | 0 | [] → [1] | |
| 16 | dfs(1, [1]) — exclude 2 | 1 | [1] | |
| 17 | dfs(2, [1]) — exclude 3 | 2 | [1] | |
| 18 | dfs(3, [1]) | 3 | [1] | append [1] → [[], [3], [2], [2,3], [1]] |
| 19 | return to dfs(2), include 3 | 2 | [1] → [1,3] | |
| 20 | dfs(3, [1,3]) | 3 | [1,3] | append [1,3] → [[], [3], [2], [2,3], [1], [1,3]] |
| 21 | backtrack → pop 3 | 2 | [1,3] → [1] | |
| 22 | return to dfs(1), include 2 | 1 | [1] → [1,2] | |
| 23 | dfs(2, [1,2]) — exclude 3 | 2 | [1,2] | |
| 24 | dfs(3, [1,2]) | 3 | [1,2] | append [1,2] → [[], [3], [2], [2,3], [1], [1,3], [1,2]] |
| 25 | return to dfs(2), include 3 | 2 | [1,2] → [1,2,3] | |
| 26 | dfs(3, [1,2,3]) | 3 | [1,2,3] | append [1,2,3] → [[], [3], [2], [2,3], [1], [1,3], [1,2], [1,2,3]] |
| 27 | backtrack → pop 3 | 2 | [1,2,3] → [1,2] | |
| 28 | backtrack → pop 2 | 1 | [1,2] → [1] | |
| 29 | backtrack → pop 1 | 0 | [1] → [] | |
| 30 | recursion ends | — | — | ✅ final result |
- Solution 2:
| num | res (before) | new subsets | res (after) |
|---|---|---|---|
| 1 | [[]] |
[[1]] |
[[], [1]] |
| num | res (before) | new subsets | res (after) |
|---|---|---|---|
| 2 | [[], [1]] |
[[2], [1,2]] |
[[], [1], [2], [1,2]] |
| num | res (before) | new subsets | res (after) |
|---|---|---|---|
| 3 | [[], [1], [2], [1,2]] |
[[3], [1,3], [2,3], [1,2,3]] |
[[], [1], [2], [1,2], [3], [1,3], [2,3], [1,2,3]] |
- Solution 3: [000, 001, 010, 011, 100, 101, 110, 111]
