Framework Thinking - Neetcode 150 - Kth Smallest Integer in BST

Here is solutions for Kth Smallest Integer in BST.

1. Understand the problem

We are given:

- The root of a Binary Search Tree (BST)

- An integer k

We must return the k-th smallest value in the BST.

Key BST Property:

For every node:

- All values in the left subtree are smaller

- All values in the right subtree are larger

So, an inorder traversal (Left → Root → Right) of a BST gives values in sorted order.

2. Clarify constraints, asks 4 - 5 questions including edge cases.

Is k always valid?

Yes, assume 1 ≤ k ≤ number of nodes.

Are all node values unique?

Usually yes (standard BST), but solution works even with duplicates if they exist.

What is the size of the tree?

Up to 10^4 – 10^5 nodes (typical LeetCode constraint).

Tree shape?

Can be skewed (like a linked list) or balanced.

Recursive solution allowed?

Yes, but space complexity may matter in worst case.

3. Explore examples.

Example 1:

Input: root = [3,1,4,null,2], k = 1

    3
   / \
  1   4
   \
    2

Inorder Traversal → [1, 2, 3, 4]
k = 1 → Answer = 1

Example 2:

Input: root = [5,3,6,2,4,null,null,1], k = 3

Inorder → [1, 2, 3, 4, 5, 6]
k = 3 → Answer = 3

4. Brainstorm 2 - 3 solutions, naive solution first and optimize later. Explain the key idea of each solution.

4.1. Solution 1: Full Inorder Traversal - Time O(N), Space O(N)

Idea:
- Do inorder traversal.
- Store values in a list.
- Return list[k-1].
Time: O(n)
Space: O(n)

4.2. Solution 2: Inorder Traversal with Early Stop (Optimized) - Time O(k), space O(H)

Idea:

Traverse inorder.
Keep a counter.
When counter == k → return result immediately.

No need to store full array.

Time: O(k) average, O(n) worst
Space: O(h) (recursion stack)

4.3. Iterative Inorder Using Stack - Time O(k), space O(H)

Idea:
- Simulate recursion using a stack.
- Push all left nodes.
- Pop nodes one by one.
- Decrement k.
- When k == 0, return the node value.
Time: O(k) average
Space: O(h)

5. Implement solutions.

5.1. Very Naive Solution - Time O(NlogN), Space O(N)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        arr = []

        def dfs(node):
            if not node:
                return

            arr.append(node.val)
            dfs(node.left)
            dfs(node.right)

        dfs(root)
        arr.sort()
        return arr[k - 1]

Time: O(NlogN).
Space: O(N).

5.2. Naive Solution - Time O(N), Space O(N)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        arr = []

        def dfs(node):
            if not node:
                return

            dfs(node.left)
            arr.append(node.val)
            dfs(node.right)

        dfs(root)
        return arr[k - 1]

Time: O(N).
Space: O(N).

5.3. Recursive DFS (Optimal) - Time O(K), Space O(K) but for recursion calls

Idea: Prunning for another recursion when count = k

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        cnt = k
        res = root.val

        def dfs(node):
            nonlocal cnt, res
            if not node:
                return

            dfs(node.left)
            cnt -= 1
            if cnt == 0:
                res = node.val
                return
            dfs(node.right)

        dfs(root)
        return res

Time: O(K).
Space: O(K).

5.4. Iterative DFS (Optimal) - Time O(K), Space O(K) for stack

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        stack = []
        curr = root

        while stack or curr:
            while curr:
                stack.append(curr)
                curr = curr.left
            curr = stack.pop()
            k -= 1
            if k == 0:
                return curr.val
            curr = curr.right

Time: O(K).
Space: O(K).

5.5. Morris Traversal - Time O(N), Space O(1)

Morris Traversal is a brilliant idea because it lets you traverse a binary tree with O(1) extra space (no recursion, no stack).
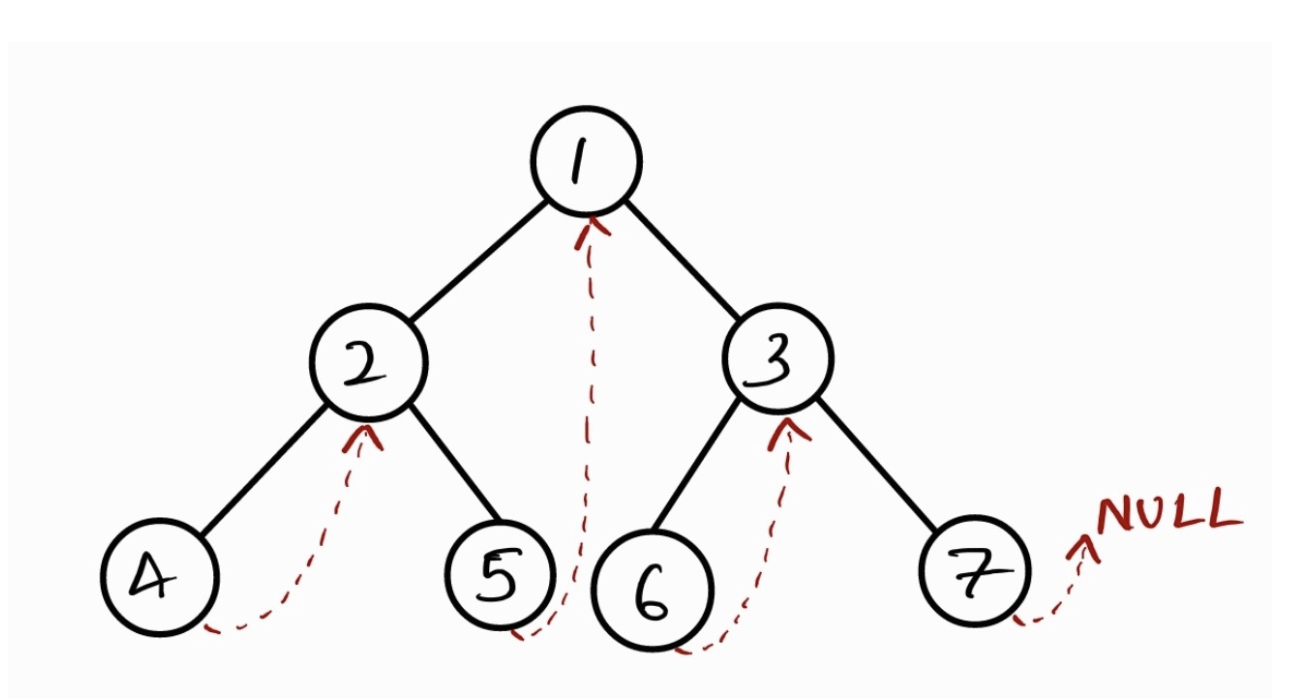
Key Idea:
- Using thread to route the traverse to successor => Idea same linked list in tree.

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right

class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        curr = root

        while curr:
            if not curr.left:
                k -= 1
                if k == 0:
                    return curr.val
                curr = curr.right
            else:
                pred = curr.left
                while pred.right and pred.right != curr:
                    pred = pred.right

                if not pred.right:
                    pred.right = curr
                    curr = curr.left
                else:
                    pred.right = None
                    k -= 1
                    if k == 0:
                        return curr.val
                    curr = curr.right

        return -1

Time: O(N).
Space: O(1)

6. Dry run testcases.

Step	Action	cur	Stack (top → right)	k	Output
0	Init	3	[]	2	–
1	push 3	1	[3]	2	–
2	push 1	None	[3, 1]	2	–
3	pop 1	1	[3]	1	–
4	move to right of 1	2	[3]	1	–
5	push 2	None	[3, 2]	1	–
6	pop 2	2	[3]	0 ✅	return 2

December 4, 2025