Framework Thinking - Neetcode 150 - Subtree of Another Tree
Here is solutions for Subtree of Another Tree.
1. Understand the problem
-
You are given two binary trees: root and subRoot. Return True if subRoot is a subtree of root**, meaning there exists a node in root such that the entire subtree starting at that node is identical to subRoot.
-
Two trees are identical if:
-
Their root values are the same.
-
Their left subtrees are identical.
-
Their right subtrees are identical.
-
-
Goal: Detect the presence of a matching subtree inside a bigger tree.
2. Clarify constraints, asks 4 - 5 questions including edge cases.
- What is the size of the trees?
- Typical LeetCode constraints: up to 10^4 nodes. This affects recursion depth and performance.
- Can subRoot be NULL?
- If subRoot is NULL → return True? (Usually Yes: empty tree is a subtree of any tree.)
- Can root be NULL while subRoot is not?
- Then → return False.
- Do values contain duplicates?
- Important because identical values don’t guarantee identical structure.
- What does “subtree” strictly mean?
- Must match both structure and values, not just existence of values.
Edge cases:
-
root = None, subRoot = None → True
-
root = None, subRoot != None → False
-
Tree with repeated values
-
Deep skewed tree causing recursion depth issues
3. Explore examples.
- Example 1
root: 3
/ \
4 5
/ \
1 2
subRoot: 4
/ \
1 2
- This matches perfectly → True
- Example 2
subRoot: 4
/ \
1 2
\
0
- This differs structurally → False
- Example 3
root: None
subRoot: None → True
4. Brainstorm 2 - 3 solutions, naive solution first and optimize later. Explain the key idea of each solution.
4.1. Solution A — Naive DFS + Tree Equality Check (Most common) - Time O(N * M), Space O(H)
Idea:
- Traverse every node in root.
- At each node, check if its subtree is identical to subRoot.
-
Time: O(N * M).
-
Space: O(H), worst case O(N)
4.2. Solution B — Serialize both trees + substring match (KMP / string search) - Time O(N + M), Space O(N + M)
Serialize tree using preorder with null markers:
3,4,1,#,#,2,#,#,5,#,#
4,1,#,#,2,#,#
-
Time: O(N + M).
-
Space: O(N + M).
5. Implement solutions.
5.1. Depth First Search (DFS) - Time (M * N), Space O(H)
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not subRoot:
return True
if not root:
return False
if self.sameTree(root, subRoot):
return True
return (self.isSubtree(root.left, subRoot) or
self.isSubtree(root.right, subRoot))
def sameTree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
if not root and not subRoot:
return True
if root and subRoot and root.val == subRoot.val:
return (self.sameTree(root.left, subRoot.left) and
self.sameTree(root.right, subRoot.right))
return False
-
Time: O(N * M).
-
Space: O(H), worst case O(N)
5.2. Serialize both trees + substring match (KMP / Z-index) - Time O(N + M), Space O(N + M)
- Z-index:
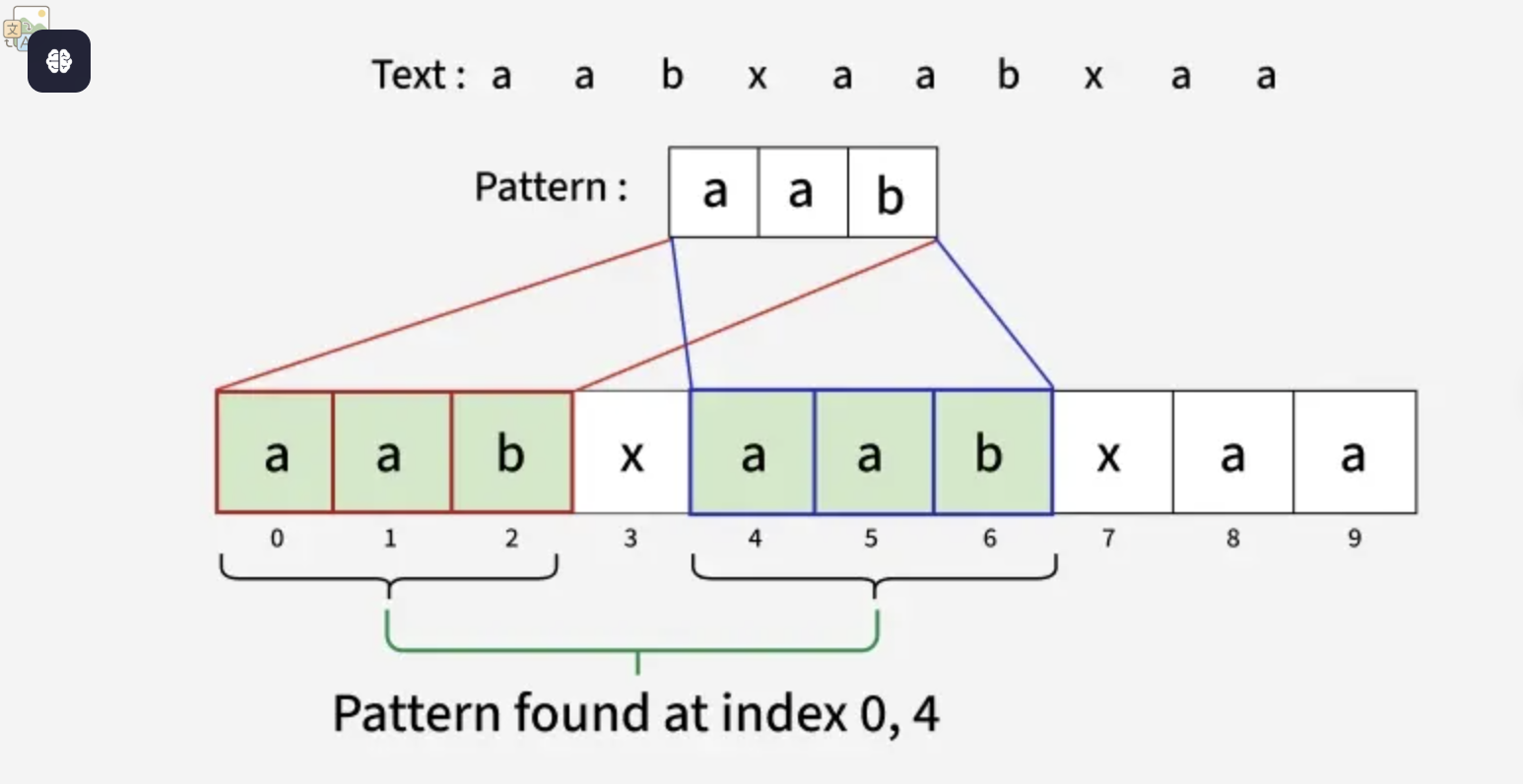
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def serialize(self, root: Optional[TreeNode]) -> str:
if root == None:
return "$#"
return ("$" + str(root.val) + self.serialize(root.left) + self.serialize(root.right))
def z_function(self, s: str) -> list:
z = [0] * len(s)
l, r, n = 0, 0, len(s)
for i in range(1, n):
if i <= r:
z[i] = min(r - i + 1, z[i - l])
while i + z[i] < n and s[z[i]] == s[i + z[i]]:
z[i] += 1
if i + z[i] - 1 > r:
l, r = i, i + z[i] - 1
return z
def isSubtree(self, root: Optional[TreeNode], subRoot: Optional[TreeNode]) -> bool:
serialized_root = self.serialize(root)
serialized_subRoot = self.serialize(subRoot)
combined = serialized_subRoot + "|" + serialized_root
z_values = self.z_function(combined)
sub_len = len(serialized_subRoot)
for i in range(sub_len + 1, len(combined)):
if z_values[i] == sub_len:
return True
return False
-
Time: O(N + M).
-
Space: O(N + M).
- KMP:
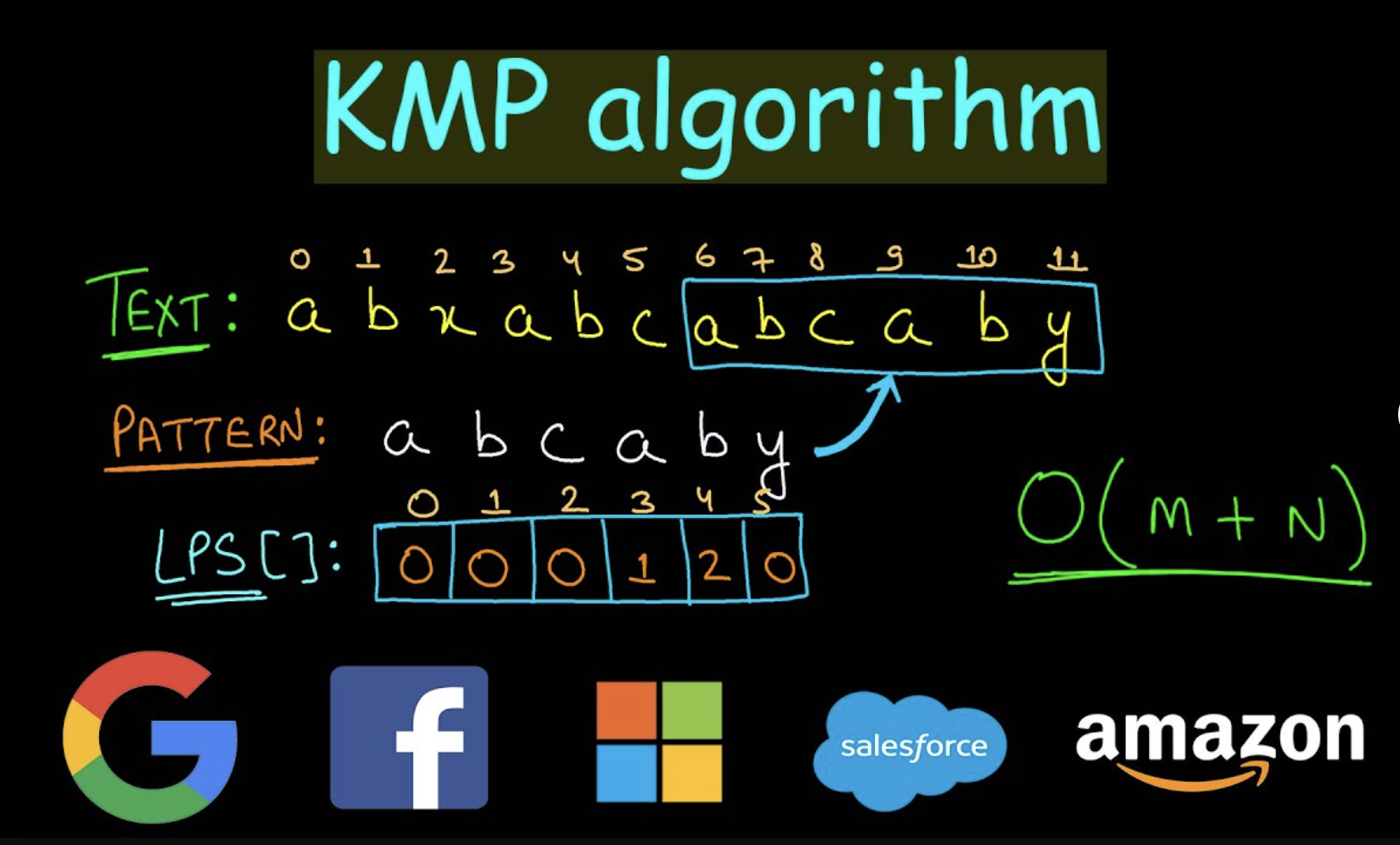
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def serialize(self, root):
if root is None:
return "$#"
return "$" + str(root.val) + self.serialize(root.left) + self.serialize(root.right)
# Build LPS array for KMP
def build_lps(self, pattern):
lps = [0] * len(pattern)
length = 0 # length of longest prefix-suffix
i = 1
while i < len(pattern):
if pattern[i] == pattern[length]:
length += 1
lps[i] = length
i += 1
else:
if length != 0:
length = lps[length - 1]
else:
lps[i] = 0
i += 1
return lps
# KMP substring search
def kmp_search(self, text, pattern):
if not pattern:
return True
lps = self.build_lps(pattern)
i = 0 # text index
j = 0 # pattern index
while i < len(text):
if text[i] == pattern[j]:
i += 1
j += 1
if j == len(pattern):
return True # match found
else:
if j != 0:
j = lps[j - 1]
else:
i += 1
return False
def isSubtree(self, root, subRoot):
serialized_root = self.serialize(root)
serialized_subRoot = self.serialize(subRoot)
return self.kmp_search(serialized_root, serialized_subRoot)
-
Time: O(N + M).
-
Space: O(N + M).
6. Dry run testcases.
root: subRoot:
3 4
/ \ / \
4 5 1 2
/ \
1 2
-
isSubtree(3, 4) -> False
-
isSubtree(4, 4) OR isSubtree(5, 4)
-
isSameTree(4, 4) → ✅
Note: isSameTree(root, subRoot) must call the left and child, but not only a.val != b.val.
