Coding Interview Template
Here is the template for coding interview patterns
1. Two Pointer
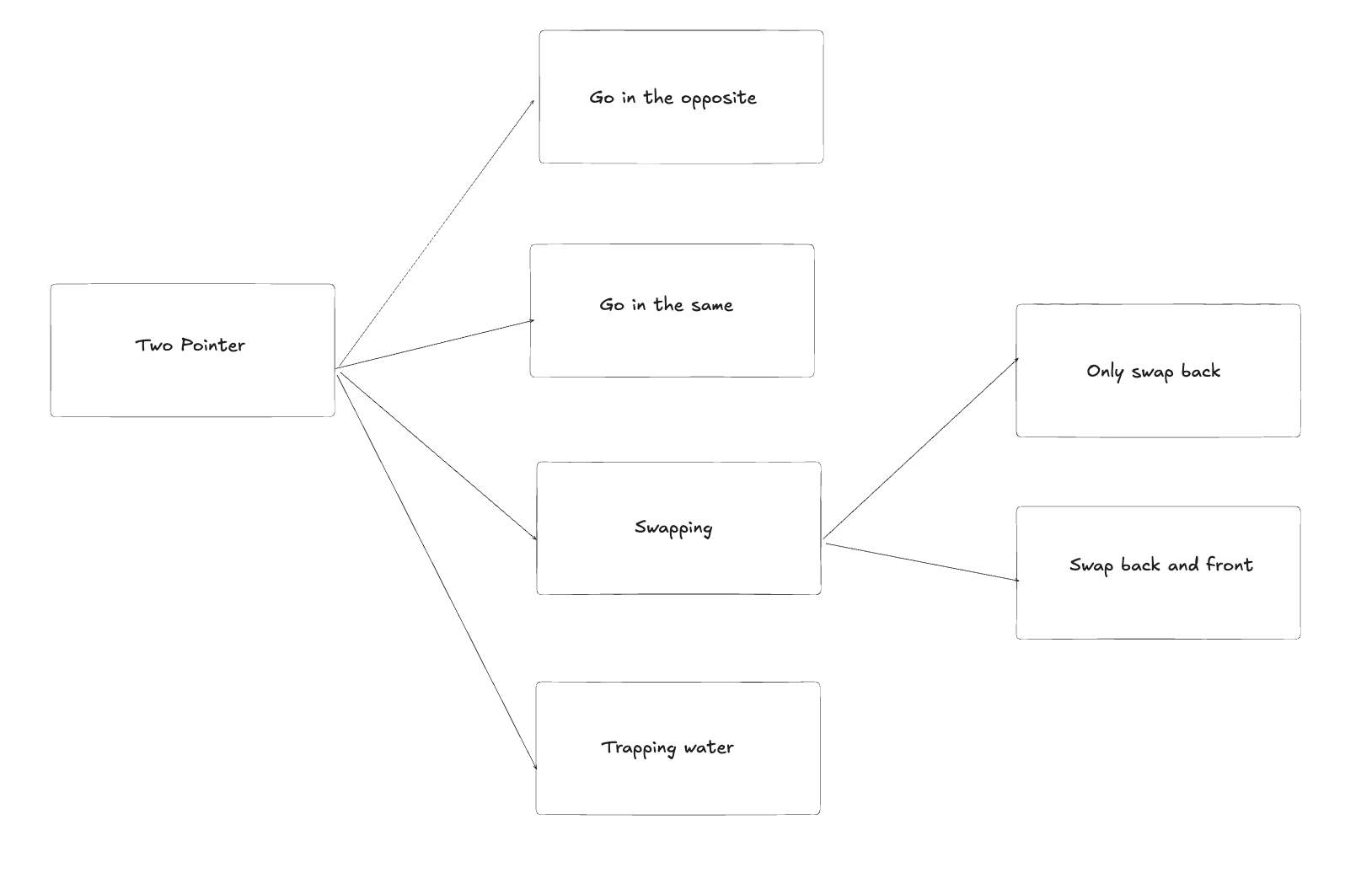
1.1. Go in the opposite
- Step 1: Giống binary search nhưng mà không dùng mid
Sample:
def twoSum(nums, target):
left, right = 0, len(nums) - 1
while left < right:
current_sum = nums[left] + nums[right]
if current_sum == target:
return True
if current_sum < target:
left += 1
else:
right -= 1
return False
1.2. 3-Sum (Keep one number -> 2-Sum):
- Step 1: Keep nums[i] and follow 2 sum pattern.
Sample:
class Solution:
def triangleNumber(self, nums: List[int]):
nums.sort()
n = len(nums)
count = 0
for end in range(n - 1, -1, -1):
target = nums[end]
left, right = 0, end - 1
while left < right:
curr_sum = nums[left] + nums[right]
if curr_sum > target:
count += right - left # Node here (Keep right)
right -= 1
else:
left += 1
return count
1.3. Go in the same
-
Step 1: Go from left to right.
-
Step 2: Init nextNonDup.
-
Step 3: If meet condition => Increase nextNonDup in condition.
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
nextNonDup = 0
n = len(nums)
for i in range(n):
if i == 0 or nums[i] != nums[nextNonDup - 1]:
nums[nextNonDup] = nums[i]
nextNonDup += 1
return nextNonDup
1.4. Swapping
1.4.1. Swap to back
-
Step 1: Go from left to right.
-
Step 2: Init nextNonZeros.
-
Step 3: If meet nums[i] == 0 => Swap it back => Increase nextNonZeros in condition.
class Solution:
def moveZeroes(self, nums: List[int]):
n = len(nums)
nextNonZeros = 0
for i in range(n):
if nums[i] != 0:
nums[i], nums[nextNonZeros] = nums[nextNonZeros], nums[i]
nextNonZeros += 1
return nums
1.4.2. Swap back and front
-
Step 1: Go from left and right, init counter i
-
Step 2: If get nums[i] == 0 => Swap left, if get nums[i] == 1, increase i += 1. Only i += 1 when swap left
-
Step 3: If get nums[i] == 2, swap to right.
class Solution:
def sortColors(self, nums: List[int]):
left, right = 0, len(nums) - 1
i = 0
while i <= right:
if nums[i] == 0:
nums[i], nums[left] = nums[left], nums[i]
left += 1
i += 1
elif nums[i] == 1:
i += 1
else:
nums[i], nums[right] = nums[right], nums[i]
right -= 1
return nums
1.5. Trapping water
- Step 1: Count the gap between left and right.
- Step 2: Count value by leftMax and rightMax.
class Solution:
def trappingWater(self, heights: List[int]):
if not heights:
return 0
left, right = 0, len(heights) - 1
leftMax, rightMax = heights[left], heights[right]
count = 0
while left < right:
if rightMax > leftMax:
left += 1
if heights[left] > leftMax:
leftMax = heights[left]
else:
count += leftMax - heights[left]
else:
right -= 1
if heights[right] > rightMax:
rightMax = heights[right]
else:
count += rightMax - heights[right]
return count
2. Sliding Window
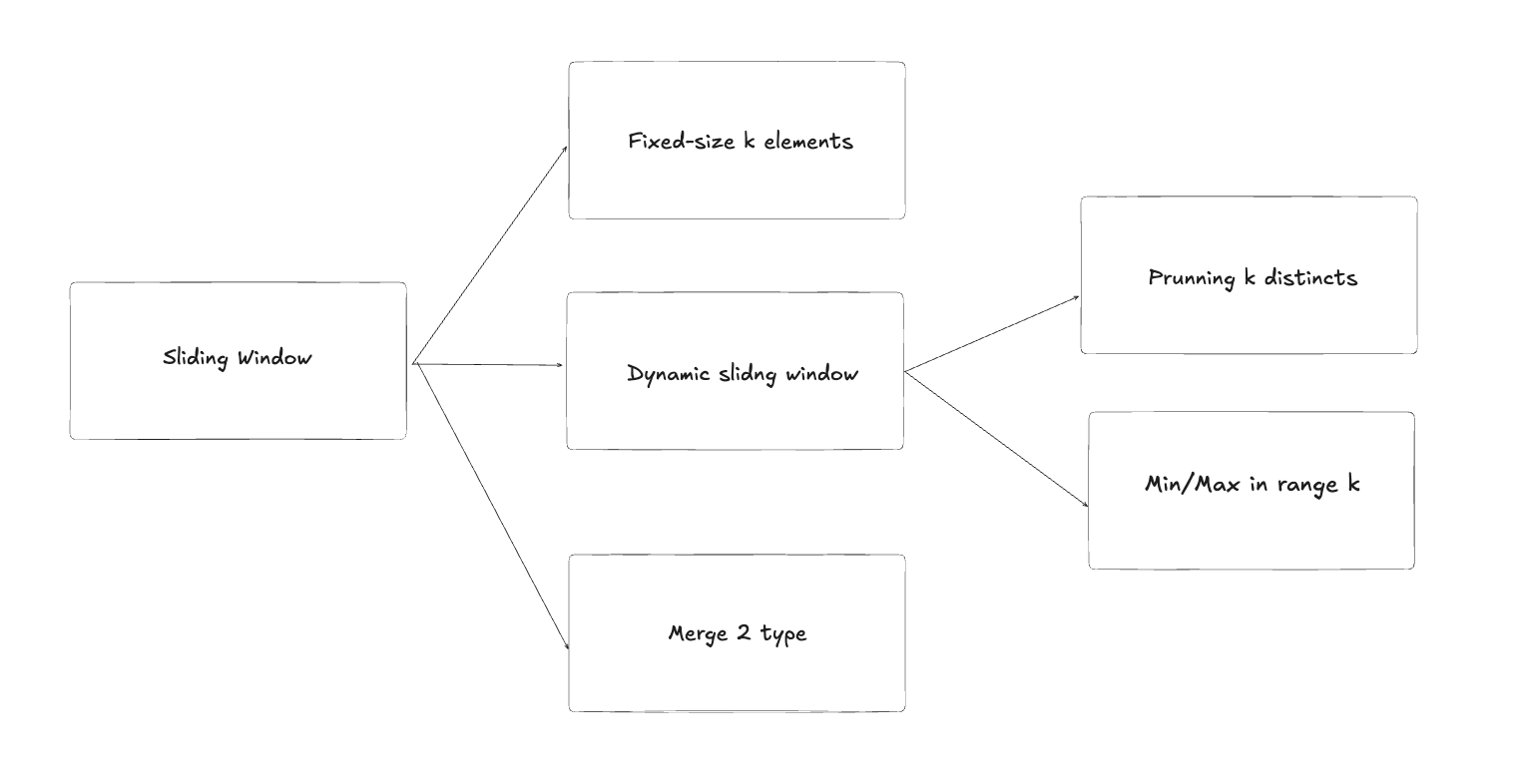
2.1. Fixed-size k elements
-
Step 1: Loop end pointer.
-
Step 2: Counting
-
Step 3: Prunning when end - start + 1 = k.
-
Step 4: Update max_len in loop.
class Solution:
def maxSum(self, nums: List[int], k: int):
state = 0
start = 0
max_sum = 0
for end in range(len(nums)):
state += nums[end]
# Prunning
if end - start + 1 == k:
# Update max here
max_sum = max(max_sum, state)
state -= nums[start]
start +=1
return max_sum
2.2. Prunning k distincts
-
Step 1: Loop end pointer.
-
Step 2: Counting.
-
Step 3: Prunning from start when reach the length => Increase start.
-
Step 4: Find maximum outside the loop.
Sample:
class Solution:
def longestSubstringWithoutRepeat(self, s: str):
k = 1
# Init start
start = 0
state = {}
n = len(s)
max_len = 0
# Loop end
for end in range(n):
# Counting
state[s[end]] = state.get(s[end], 0) + 1
while state[s[end]] > k:
state[s[start]] -= 1
if state[s[start]] == 0:
del state[s[start]]
start += 1
max_len = max(max_len, end - start + 1)
return max_len
2.3. Min/Max in range k
-
Step 1: Loop end pointer.
-
Step 2: Counting
-
Step 3: Prunning when reach the condition including max_freq, (e.g. end - start + 1 - max_freq > k) => Increase start.
-
Step 4: Find max_len outside.
```pythonclass Solution: def characterReplacement(self, s: str, k: int): state = {} start = 0 max_len = 0 max_freq = 0
# Loop end
for end in range(len(s)):
state[s[end]] = state.get(s[end], 0) + 1
max_freq = max(max_freq, state[s[end]])
while (end - start + 1 - max_freq) > k:
state[s[start]] -= 1
if state[s[start]] == 0:
del(state[s[start]])
start += 1
max_len = max(max_len, end - start + 1)
return max_len ```
2.4. Merge 2 type
-
Step 1: Priority fixed-size length k.
-
Step 2: Prunning when end - start + 1 == k
-
Step 3: Subarray length k => Handle state count in when end - start + 1 == k.
-
Step 4: Subarray length k => Update max event in loop when len(state) == k
class Solution:
def maxSum(self, nums: List[int], k: int):
state = {}
curr_sum = 0
start = 0
max_sum = 0
for end in range(len(nums)):
state[nums[end]] = state.get(nums[end], 0) + 1
curr_sum += nums[end]
# Prunning
if end - start + 1 == k:
if len(state) == k:
# Update max here
max_sum = max(max_sum, curr_sum)
curr_sum -= nums[start]
state[nums[start]] -= 1
if state[nums[start]] == 0:
del(state[nums[start]])
start += 1
return max_sum
3. Linked List
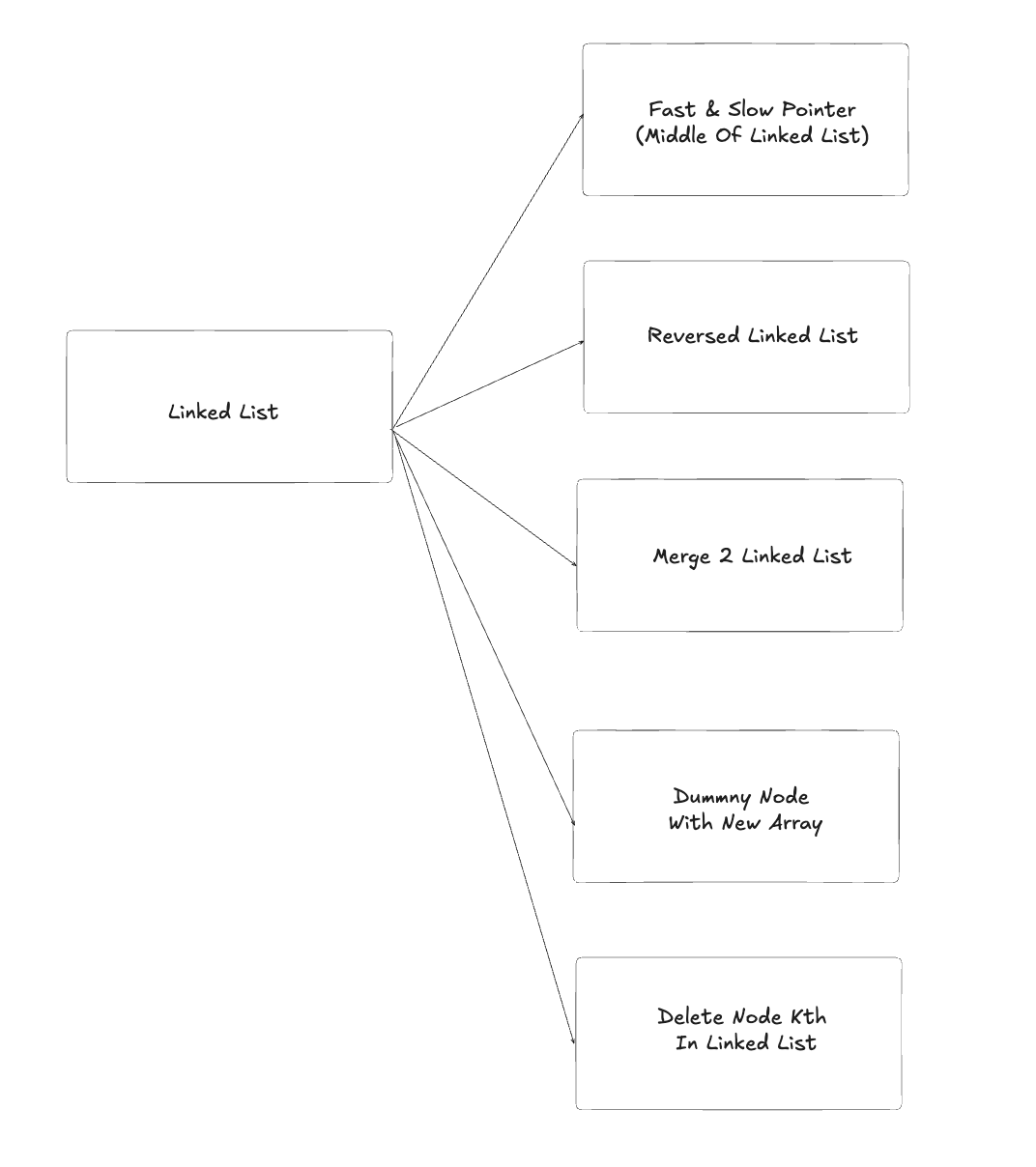
3.1. Fast & Slow Pointer (Middle Of Linked List)
-
Step 1: Init slow and fast to head
-
Step 2: Điều kiện fast & fast.next.next
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
slow = head
fast = head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if slow == fast:
return True
return False
3.2. Reversed Linked List
-
Step 1: Using prev = None and current = head.
-
Step 2: Assign curr->next = prev, assign by order: prev = current, current = next.
def reverse(head):
prev = None
current = head
while current:
next_ = current.next
current.next = prev
prev = current
current = next_
return prev
3.3. Merge 2 Linked List
-
Step 1: Init head.
-
Step 2: Assign head to head of l1 or head of l2.
-
Step 3: Using tail = head, using tail to transfer the 2 linked list.
def merge_lists(l1, l2):
if not l1: return l2
if not l2: return l1
if l1.val < l2.val:
head = l1
l1 = l1.next
else:
head = l2
l2 = l2.next
tail = head
while l1 and l2:
if l1.val < l2.val:
tail.next = l1
l1 = l1.next
else:
tail.next = l2
l2 = l2.next
tail = tail.next
tail.next = l1 or l2
return head
3.4. Dummny Node With New Array
-
Step 1: Using dummy node to keep head.
-
Step 2: Using current = head to transfer.
-
Step 3: while current and current = current.next
def findLength(head):
length = 0
current = head
while current:
length += 1
current = current.next
return length
3.5. Delete Node Kth in Linked List
-
Step 1: Using current and prev
-
Step 2: Read from prev to curr:
- prev = curr
- curr = curr -> next
-
Step 3: If find value curr.val == target => prev.next = curr.next (skip curr node)
def deleteNode(head, target):
if head.val == target:
return head.next
prev = None
curr = head
while curr:
if curr.val == target:
prev.next = curr.next
break
prev = curr
curr = curr.next
return head
4. Stack
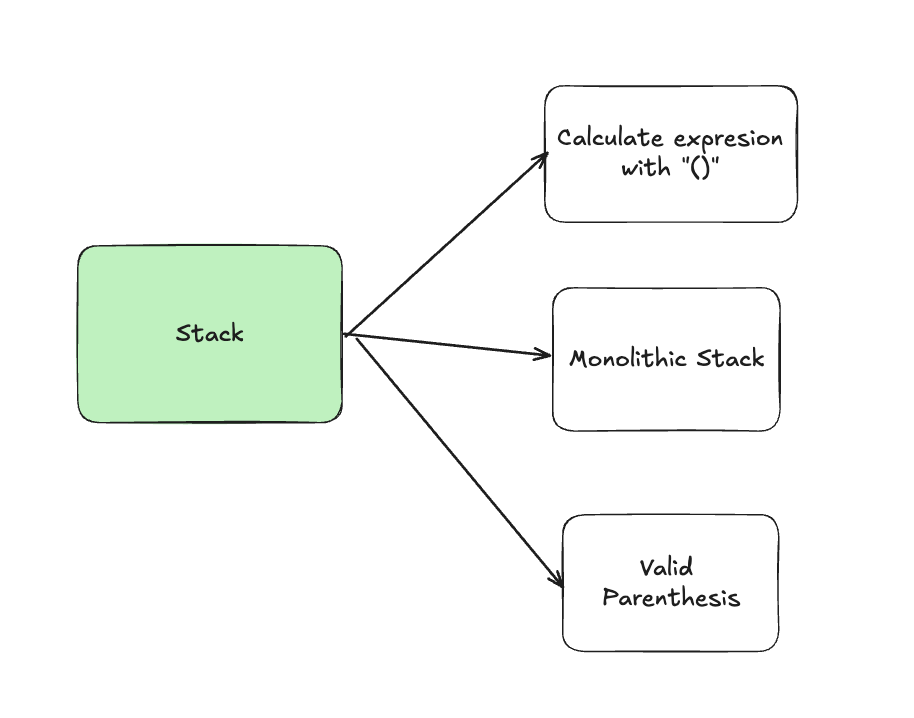
4.1. Calculate expresion with “()”
-
Step 1: Idea to calculate all the sum of stack.
-
Step 2: Assign default sign = ‘+’ => If meet negative -3 + 2
-
First sign = ‘+’ num = 0 => Add 0 to stack and sign = ‘-‘
-
When meet the second ‘+’ => it append -3 to stack
-
Next character ch = ‘2’ → updates num = 2.
-
No more characters → final operation triggere => sign = ‘+’ → stack.append(2)
-
-
Step 3: If meet ‘(‘ => recursive to count sum and break when meet ‘)’.
class Solution:
def calculate(self, s: str) -> int:
def helper(chars):
num = 0
sign = '+'
stack = []
while chars:
ch = chars.pop(0)
if ch.isdigit():
num = num * 10 + int(ch)
if ch == '(':
num = helper(chars)
# not digit -> sign or not chars
if ch in '+-*/)' or not chars:
if sign == '+':
stack.append(num)
elif sign == '-':
stack.append(-num)
elif sign == '*':
stack.append(stack.pop() * num)
elif sign == '/':
prev = stack.pop()
stack.append(int(prev / num)) # Truncate toward zero
sign = ch
num = 0
if ch == ')':
break
return sum(stack)
return helper(list(s))
4.2. Evaluation of Postfix Expression
-
Step 1: If meet digit build it.
-
Step 2: If you find the character => calculate and add to stack
-
Step 3: Using stack sau / track trước
def evaluate_postfix(expression):
stack = []
tokens = expression.split()
for token in tokens:
if token.isdigit():
stack.append(int(token))
else:
b = stack.pop()
a = stack.pop()
if token == '+':
stack.append(a + b)
elif token == '-':
stack.append(a - b)
elif token == '*':
stack.append(a * b)
elif token == '/':
stack.append(int(a / b)) # Integer division
return stack[0]
4.3. Monolithic Stack
-
Step 1: Loop from left to right, append i to stack.
-
Step 2: if nums[i] > nums[stack[-1]] => Update index of the greater element of the last stack is nums[i]
def nextGreaterElement(nums):
n = len(nums)
result = [-1] * n
stack = []
for i in range(n):
while stack and nums[i] > nums[stack[-1]]:
idx = stack.pop()
result[idx] = nums[i]
stack.append(i)
return result
4.4. Longest Valid Parenthesis
-
Step 1: If find ‘(‘ add to stack.
-
Step 2: Else check prefix is ‘(‘ => pop the stack => Update max.
-
Step 3: Else append it to stack.
class Solution:
def longestValidParentheses(self, s: str) -> int:
max_len = 0
# Magic here to trick case ()
# Store last index of '('
stack = [-1]
for i, char in enumerate(s):
if char == '(':
stack.append(i)
else:
stack.pop()
if stack:
max_len = max(max_len, i - stack[-1])
else:
stack.append(i)
return max_len
5. CPU Scheduling
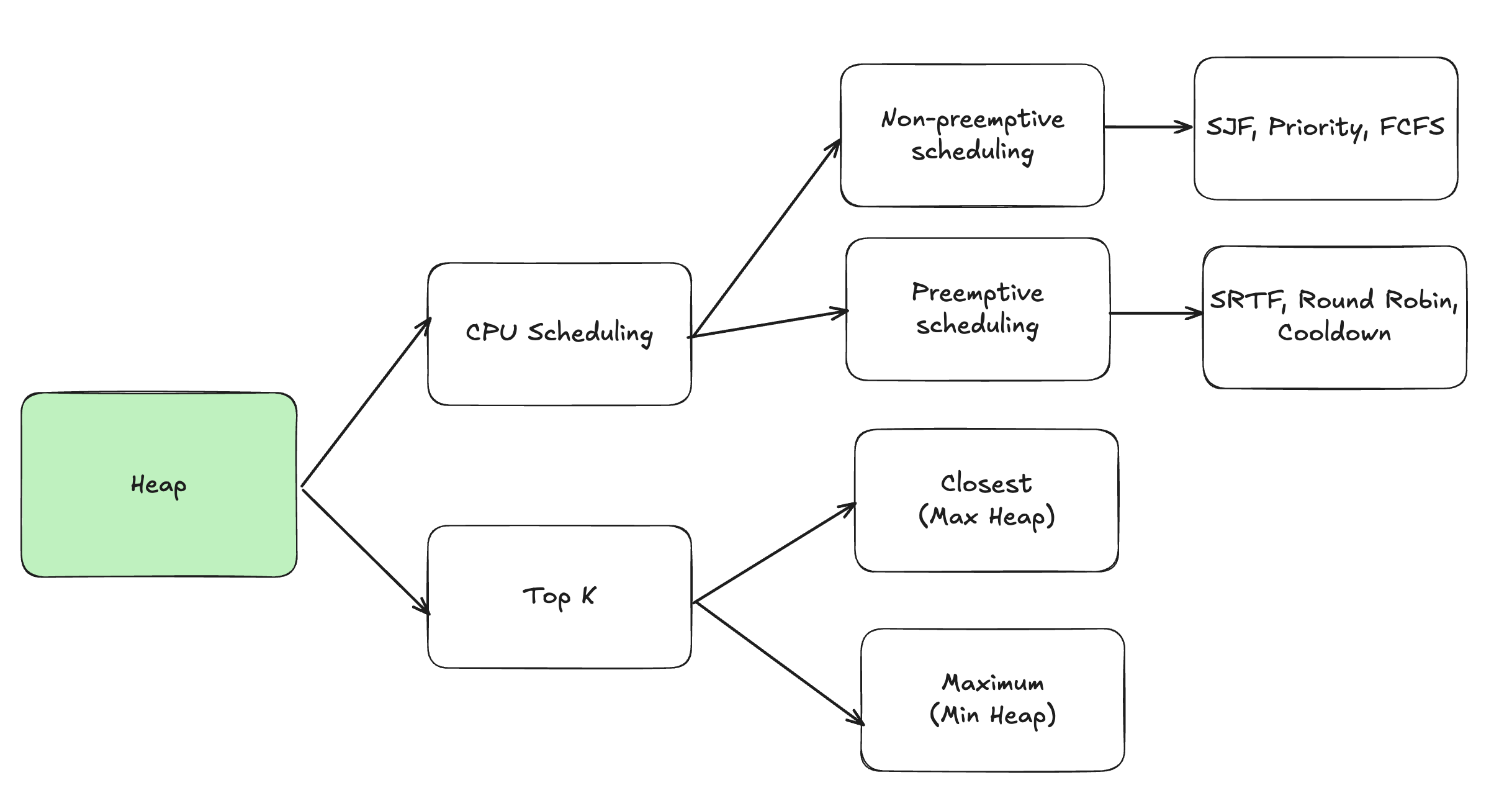
5.1. Non-preemptive scheduling
5.1.1. SJF - Shortest Job First
-
Step 1: Sort by start_time, init time, schedule.
-
Step 2: Init ready tasks.
-
Step 3: Init when i < n or ready tasks.
-
Step 4: while i < n and tasks[i][‘arrival_time’] <= time => Push to ready heap => Order by burst_time (tasks[i][‘burst_time’],…)
-
Step 5: If ready have tasks => Process it. Else time = start of the tasks.
import heapq
def sjf(tasks):
tasks.sort(key=lambda x:x['arrival_time'])
# Base
time = 0
schedule = []
# Add them
i = 0
ready = []
n = len(tasks)
while i < n or ready:
while i < n and tasks[i]['arrival_time'] <= time:
heapq.heappush(ready, (tasks[i]['burst_time'], tasks[i]['arrival_time'], tasks[i]['pid'], tasks[i]))
i += 1
if ready:
_, _, _, task = heapq.heappop(ready)
start_time = time
end_time = start_time + task['burst_time']
schedule.append((task['pid'], start_time, end_time))
time = end_time
else:
time = tasks[i]['arrival_time']
return schedule
# Sample test case
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 8},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 4},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 9},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 5}
]
result = sjf(tasks)
for pid, start, end in result:
print(f"Task {pid}: Start at {start}, End at {end}")
5.1.2. Priority Scheduling
-
Step 1: Sort by start_time, init time, schedule.
-
Step 2: Init ready tasks.
-
Step 3: Init when i < n or ready tasks.
-
Step 4: while i < n and tasks[i][‘arrival_time’] <= time => Push to ready heap => Order by (tasks[i][‘priority’],…)
-
Step 5: If ready have tasks => Process it. Else time = start of the tasks.
import heapq
def priority_scheduling(tasks):
# Sort by arrival time first
tasks.sort(key=lambda x: x['arrival_time'])
time = 0
i = 0
n = len(tasks)
schedule = []
ready = []
while i < n or ready:
# Push all tasks that have arrived into the ready queue
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready, (task['priority'], task['arrival_time'], task['pid'], task))
i += 1
if ready:
_, _, _, task = heapq.heappop(ready)
start = time
end = start + task['burst_time']
schedule.append((task['pid'], start, end))
time = end
else:
# If no task is ready, jump to the next arrival
time = tasks[i]['arrival_time']
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 10, 'priority': 3},
{'pid': 'P2', 'arrival_time': 2, 'burst_time': 5, 'priority': 1},
{'pid': 'P3', 'arrival_time': 1, 'burst_time': 8, 'priority': 2},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 6, 'priority': 4}
]
result = priority_scheduling(tasks)
for pid, start, end in result:
print(f"Task {pid}: Start at {start}, End at {end}")
5.1.3. FCFS - First Come First Serve
-
Step 1: Sort by start_time, init time, schedule.
-
Step 2: Loop task in tasks.
-
Step 3: Update schedule.
-
Step 4: Update time = curr_time + burst_time, time = end_time.
-
Step 5: if time < task[‘arrival_time’]: time = task[‘arrival_time’]
def fcfs(tasks):
# Task
tasks.sort(key=lambda x:x['arrival_time'])
# Time
time = 0
schedule = []
for task in tasks:
if time < task['arrival_time']:
time = task['arrival_time']
start_time = time
end_time = time + task['burst_time']
schedule.append((task['pid'], start_time, end_time))
time = end_time
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 5},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 1},
]
print(fcfs(tasks))
5.1.4. Max CPU Load
-
Step 1: Init time, schedule.
-
Step 2: For job in jobs
-
Step 3: Auto add jobs to queue => count max_cpu_load outside.
-
Step 4: While time have pass end tasks => pop it out heap
import heapq
def find_max_cpu_load(jobs):
# Sort jobs
jobs.sort(key=lambda x:x[0])
process_tasks = []
# CPU load
max_cpu_load = 0
curr_cpu_load = 0
for job in jobs:
start, end, load = job
while process_tasks and process_tasks[0][0] <= start:
processed_job = heapq.heappop(process_tasks)
curr_cpu_load -= processed_job[1]
# Append to jobs to queue by start_time
heapq.heappush(process_tasks, (end, load))
# Update max_cpu_load
curr_cpu_load += load
max_cpu_load = max(max_cpu_load, curr_cpu_load)
return max_cpu_load
jobs = [(1, 4, 3), (2, 5, 4), (7, 9, 6)]
print(find_max_cpu_load(jobs))
5.2. Preemptive scheduling
5.2.1. SRTF - Shortest Remaining Time First (SJF + Remaining)
-
Step 1: Sort by start_time, init time, schedule, add ‘remaining’: t[‘burst_time’].
-
Step 2: Init ready tasks, priority by remaining time.
-
Step 3: Init completed = 0, last_pid => to detect when the running process has changed, start_time => marks when a process starts (or resumes) execution
-
Step 4: Loop when completed < n or ready.
-
Step 5: While i < n and tasks[i][‘arrival_time’] <= time => Add ‘remaining_time’ to tasks.
-
Step 6: If ready => task[‘remaining’] -= 1, time += 1, update last_pid.
-
Step 7: if pid != last_pid, next task is the last_pid but last_pid is not None => add the remaining tasks last_pid to heap.
import heapq
def srtf(tasks):
# Preprocess: add 'remaining' field and sort by arrival
tasks = sorted([{**t, 'remaining': t['burst_time']} for t in tasks], key=lambda x: x['arrival_time'])
time = 0
i = 0
n = len(tasks)
ready = [] # (remaining_time, arrival_time, pid, task)
schedule = []
completed = 0
last_pid = None
start_time = None
while completed < n or ready:
# Push all tasks that have arrived into the ready
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready, (task['remaining'], task['arrival_time'], task['pid'], task))
i += 1
if ready:
_, _, pid, task = heapq.heappop(ready)
if pid != last_pid:
# Job cu chua xong
if last_pid is not None:
schedule.append((last_pid, start_time, time))
start_time = time
last_pid = pid
# Execute task for 1 time unit
task['remaining'] -= 1
time += 1
if task['remaining'] > 0:
heapq.heappush(ready, (task['remaining'], task['arrival_time'], task['pid'], task))
else:
completed += 1
schedule.append((pid, start_time, time))
last_pid = None
else:
time += 1
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 8},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 4},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 9},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 5}
]
for pid, start, end in srtf(tasks):
print(f"Task {pid}: Start at {start}, End at {end}")
5.2.2. Round Robin (FCFS + Remaining)
-
Step 1: Sort by start_time, init time, schedule, add ‘remaining’: t[‘burst_time’].
-
Step 2: Init completed = 0, ready => different than FCFS because to store remaining tasks.
-
Step 3: while completed < n or ready
-
Step 4: while i < n and tasks[i][‘arrival_time’] <= time => ready.append(tasks[i]).
-
Step 5: If ready handle tasks + push remaning tasks to queue => schedule.append((task[‘pid’], start_time, time + min(quantum, task[‘remaining’])))
-
Step 6: Remember to push tasks come from the time while the current tasks is executed => while i < n and tasks[i][‘arrival_time’] <= time => ready.append(tasks[i])
-
Step 7: Count completed += 1 when the tasks in compleeted.
-
Step 8: If not is queue => time = tasks[i][‘arrival_time’].
from collections import deque
def round_robin(tasks, quantum):
# Add remaining time to each task
tasks = sorted([{**t, 'remaining': t['burst_time']} for t in tasks], key=lambda x: x['arrival_time'])
time = 0
schedule = []
i = 0 # Index for incoming tasks
n = len(tasks)
completed = 0
ready = deque()
while completed < n or ready:
# Enready tasks that have arrived
while i < n and tasks[i]['arrival_time'] <= time:
ready.append(tasks[i])
i += 1
if ready:
task = ready.popleft()
start_time = time
duration = min(quantum, task['remaining'])
time += duration
task['remaining'] -= duration
schedule.append((task['pid'], start_time, time))
# But while that task was executing, new tasks might have arrived
while i < n and tasks[i]['arrival_time'] <= time:
ready.append(tasks[i])
i += 1
# If not finished, push back to ready
if task['remaining'] > 0:
ready.append(task)
else:
completed += 1
else:
# No ready task, jump to the next arrival time
if i < n:
time = tasks[i]['arrival_time']
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 5},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 8},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 6}
]
quantum = 3
result = round_robin(tasks, quantum)
for pid, start, end in result:
print(f"Task {pid}: Start at {start}, End at {end}")
5.2.3. Cooldown
-
Step 1: Count the frequence of the jobs, do longer jobs first.
-
Step 2: Init time, schedule
-
Step 3: Init ready (max_heap) and cooldown deque.
-
Step 4: while ready or cooldown:
-
Step 5: If have ready => Process tasks in ready => Add remaining task to cool down at time + n + 1 => cooldown.append((time + n + 1, cnt + 1)).
-
Step 6: If have cooldown and come to time cooldown at cooldown[0][0] == time => Push cooldown tasks to ready task: heapq.heappush(ready, cooldown.popleft()[1])
import heapq
from collections import Counter, deque
from typing import List
class Solution:
def leastInterval(self, tasks: List[str], n: int) -> int:
# Count the frequency of tasks
freq = Counter(tasks)
# Python's heapq is a min-heap, so we store negative frequencies for max-heap behavior
ready = [-cnt for cnt in freq.values()]
heapq.heapify(ready)
# Queue to manage cooldowns: (ready_time, -task_count)
cooldown = deque()
time = 0
while ready or cooldown:
time += 1
# Release from cooldown if task is ready
if cooldown and cooldown[0][0] == time:
heapq.heappush(ready, cooldown.popleft()[1])
if ready:
cnt = heapq.heappop(ready)
if cnt + 1 < 0:
# Add to cooldown queue with ready time = now + n + 1
cooldown.append((time + n + 1, cnt + 1))
return time
5.3. Top-K
5.3.1. Closest (Max Heap)
-
Step 1: Init max heap
-
Step 2: Loop for number
-
Step 3: If len < k => heappush.
-
Step 4: Else if len > k and distance < -heap[0][0] => heappushpop.
import heapq
class Solution:
def kClosest(self, points: List[List[int]], k: int):
heap = []
for point in points:
x, y = point
distance = x * x + y * y
if len(heap) < k:
heapq.heappush(heap, (-distance, point))
elif distance < -heap[0][0]:
heapq.heappushpop(heap, (-distance, point))
return [item[1] for item in heap]
5.3.2. Maximum (Min Heap)
-
Step 1: Init min heap
-
Step 2: Loop for number
-
Step 3: If len < k => heappush.
-
Step 4: Else if len > k and num > heap[0] => heappushpop.
class Solution:
def kthLargest(self, nums: List[int], k: int):
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, num)
elif num > heap[0]:
heapq.heappushpop(heap, num)
return heap[0]
5.4. Multiple CPUs
5.4.1. FCFS Multiple CPUs
-
Step 1: Sort by start_time, init time, schedule.
-
Step 2: Init cpu_heap [(0, cpu_id) for cpu_id in range(cpu_count)].
-
Step 3: Loop task in tasks.
-
Step 4: Get earliest available CPU, start_time = max(cpu_available_time, arrival)
-
Step 5: schedule.append({‘pid’: pid, ‘cpu’: cpu_id, ‘start_time’: start_time, ‘end_time’: end_time})
-
Step 6: Push end_time to CPU heapq.heappush(cpu_heap, (end_time, cpu_id))
import heapq
def fcfs_multi_cpu(tasks, cpu_count):
# Sort tasks by arrival time
tasks = sorted(tasks, key=lambda x: x['arrival_time'])
# Min-heap of (available_time, cpu_id)
cpu_heap = [(0, cpu_id) for cpu_id in range(cpu_count)]
heapq.heapify(cpu_heap)
schedule = []
for task in tasks:
arrival = task['arrival_time']
burst = task['burst_time']
pid = task['pid']
# Get the earliest available CPU
available_time, cpu_id = heapq.heappop(cpu_heap)
# The task starts at the max of CPU's available time or its own arrival
start_time = max(available_time, arrival)
end_time = start_time + burst
schedule.append({
'pid': pid,
'cpu': cpu_id,
'start_time': start_time,
'end_time': end_time
})
# Update the CPU's available time
heapq.heappush(cpu_heap, (end_time, cpu_id))
return schedule
# Example
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 5},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 1},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 2},
]
result = fcfs_multi_cpu(tasks, cpu_count=2)
for entry in result:
print(entry)
5.4.2. SJF Multiple CPUs
-
Step 1: Sort by start_time, init time, schedule.
-
Step 2: Init cpu_heap [(0, cpu_id) for cpu_id in range(cpu_count)].
-
Step 3: Init ready queue
-
Step 4: Using assigned = False => Use to make sure assign all tasks for available CPU
-
Step 5: while i < n or ready or any(cpu[0] > time for cpu in cpu_heap)
-
Step 6: while i < n and tasks[i][‘arrival_time’] <= time => append tasks to heap priority task[‘burst_time’] => heapq.heappush(ready, (task[‘burst_time’]..)).
-
Step 7: Assigned task to all CPUs => while ready and cpu_heap and cpu_heap[0][0] <= time => start_time = max(time, cpu_available_time) => heapq.heappush(cpu_heap, (end_time, cpu_id))
-
Step 8: Fallback, if not CPU is ready => time = max(time + 1, min(tasks[i][‘arrival_time’], cpu_heap[0][0])).
import heapq
from typing import List, Dict, Tuple
def sjf_multi_cpu(tasks: List[Dict], k: int) -> List[Tuple[str, int, int, int]]:
tasks.sort(key=lambda x: x['arrival_time']) # sort by arrival_time
n = len(tasks)
i = 0
time = 0
ready = [] # (burst_time, arrival_time, pid, task)
cpu_heap = [] # (available_time, cpu_id)
schedule = []
# Initialize all CPUs as available at time 0
for cpu_id in range(k):
heapq.heappush(cpu_heap, (0, cpu_id))
while i < n or ready or any(cpu[0] > time for cpu in cpu_heap):
# Add tasks that have arrived by current time
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready, (task['burst_time'], task['arrival_time'], task['pid'], task))
i += 1
# Assign tasks to available CPUs
assigned = False
while ready and cpu_heap and cpu_heap[0][0] <= time:
burst_time, arrival_time, pid, task = heapq.heappop(ready)
cpu_available_time, cpu_id = heapq.heappop(cpu_heap)
start_time = max(time, cpu_available_time)
end_time = start_time + burst_time
schedule.append((pid, start_time, end_time, cpu_id))
heapq.heappush(cpu_heap, (end_time, cpu_id))
assigned = True
if not assigned:
# Advance time to next task arrival or next CPU free time
next_times = []
if i < n:
next_times.append(tasks[i]['arrival_time'])
if cpu_heap:
next_times.append(cpu_heap[0][0])
if next_times:
time = max(time + 1, min(next_times))
print("Time", time)
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 4},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 1},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 2},
{'pid': 'P5', 'arrival_time': 4, 'burst_time': 5},
]
schedule = sjf_multi_cpu(tasks, k=3)
for pid, start, end, cpu_id in schedule:
print(f"CPU{cpu_id} runs {pid} from {start} to {end}")
5.4.3. Priority Scheduling Multiple CPUs
-
Step 1: Sort by start_time, init time, schedule.
-
Step 2: Init cpu_heap [(0, cpu_id) for cpu_id in range(cpu_count)].
-
Step 3: Init ready queue
-
Step 4: Using assigned = False => Use to make sure assign all tasks for available CPU
-
Step 5: while i < n or ready or any(cpu[0] > time for cpu in cpu_heap)
-
Step 6: while i < n and tasks[i][‘arrival_time’] <= time => append tasks to heap priority task[‘priority’] => heapq.heappush(ready, (task[‘priority’]..)).
-
Step 7: Assigned task to all CPUs => while ready and cpu_heap and cpu_heap[0][0] <= time => start_time = max(time, cpu_available_time) => heapq.heappush(cpu_heap, (end_time, cpu_id))
-
Step 8: Fallback, if not CPU is ready => time = max(time + 1, min(tasks[i][‘arrival_time’], cpu_heap[0][0])).
import heapq
def priority_scheduling_multi_cpu(tasks, cpu_count):
tasks = sorted(tasks, key=lambda x: x['arrival_time'])
i = 0
time = 0
n = len(tasks)
cpu_heap = [(0, cpu_id) for cpu_id in range(cpu_count)]
heapq.heapify(cpu_heap)
ready_queue = []
schedule = []
while i < n or ready_queue:
# Add all tasks that have arrived by current time
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready_queue, (task['priority'], task['arrival_time'], task['pid'], task))
i += 1
# Assign ready tasks to available CPUs
assigned = False
while ready_queue and cpu_heap and cpu_heap[0][0] <= time:
cpu_available_time, cpu_id = heapq.heappop(cpu_heap)
_, arrival, pid, task = heapq.heappop(ready_queue)
start_time = max(cpu_available_time, arrival, time)
end_time = start_time + task['burst_time']
schedule.append({
'pid': pid,
'cpu': cpu_id,
'start_time': start_time,
'end_time': end_time
})
heapq.heappush(cpu_heap, (end_time, cpu_id))
assigned = True
# If no task is assigned and no CPU is available yet, move time forward
if not assigned:
next_arrival = tasks[i]['arrival_time'] if i < n else float('inf')
next_cpu_free = cpu_heap[0][0] if cpu_heap else float('inf')
# Move to the next event (task arrival or CPU becomes free)
time = max(time + 1, min(next_arrival, next_cpu_free))
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 10, 'priority': 3},
{'pid': 'P2', 'arrival_time': 2, 'burst_time': 5, 'priority': 1},
{'pid': 'P3', 'arrival_time': 1, 'burst_time': 8, 'priority': 2},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 6, 'priority': 4}
]
result = priority_scheduling_multi_cpu(tasks, cpu_count=2)
for r in result:
print(r)
6. Merge Interval
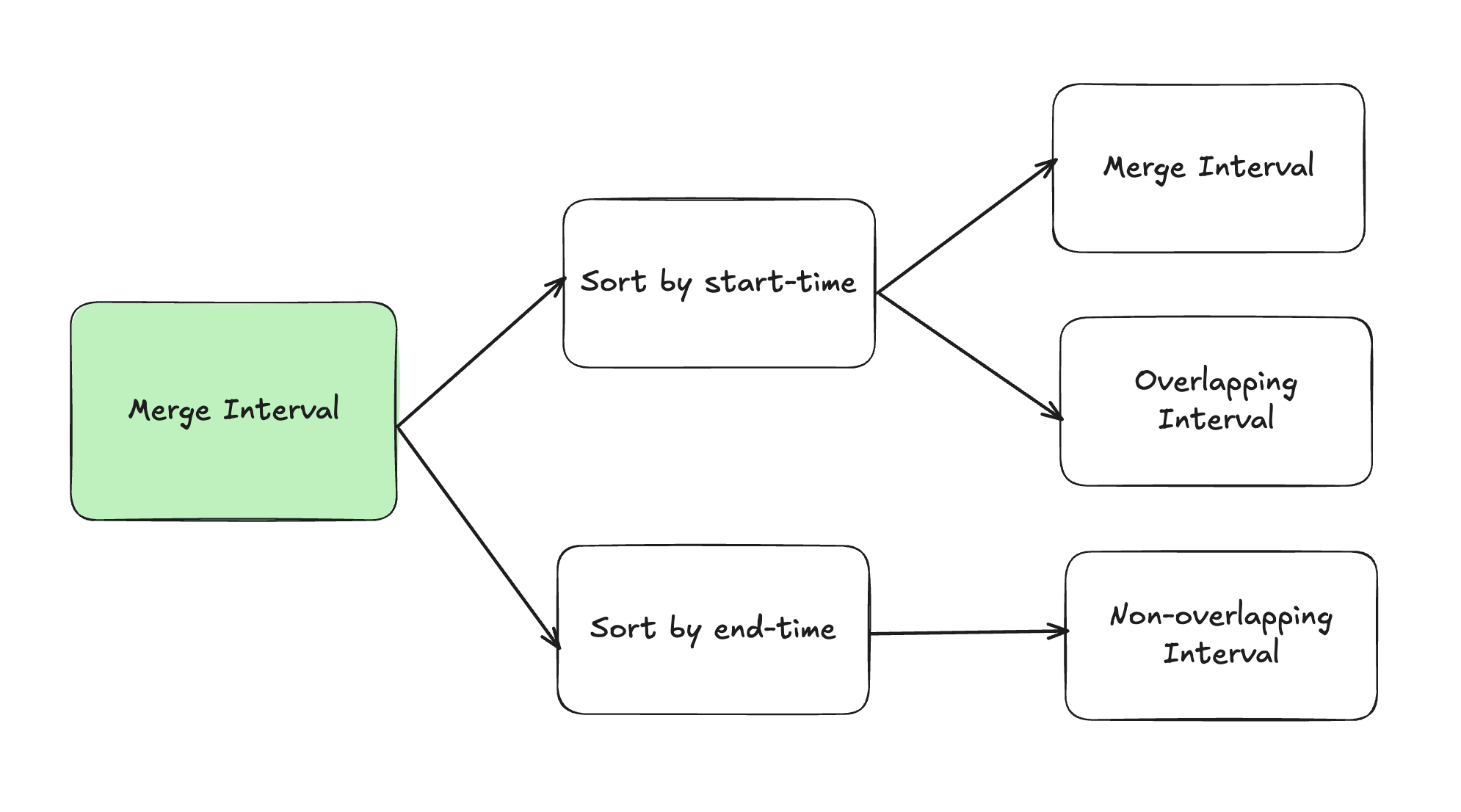
6.1. Overlapping Interval
-
Step 1: Sort by start_time.
-
Step 2: Start from (1, n) => Check if intervals[i][0] < intervals[i - 1][1] => It is overlap.
class Solution:
def canAttendMeetings(self, intervals: List[List[int]]):
# Sort by start time
intervals.sort(key=lambda x:x[0])
n = len(intervals)
# Check validate
for i in range(1, n):
# Overlap
if intervals[i][0] < intervals[i - 1][1]:
return False
return True
6.2. Merge Interval
-
Step 1: Sort by start_time.
-
Step 2: Start from (1, n) => Check if intervals[i][0] < intervals[i - 1][1] => Merge by update the end of last list => merged[-1][1] = max(interval[1], merged[-1][1])
-
Step 3: Else append to the list => merged.append(interval)
def mergeIntervals(intervals):
sortedIntervals = sorted(intervals, key=lambda x: x[0])
merged = []
for interval in sortedIntervals:
if not merged or interval[0] > merged[-1][1]:
merged.append(interval)
else:
merged[-1][1] = max(interval[1], merged[-1][1])
return merged
6.3. Non-overlapping Interval
-
Step 1: Sort by end_time.
-
Step 2: Loop from (1, n)
-
Step 3: If start of the interval intervals[i][0] >= end => count += 1 and end = intervals[i][1] => Because sort by end, larger than overlapping.
-
Step 3: Count len(intervals) - count
def nonOverlappingIntervals(intervals):
if not intervals:
return 0
intervals.sort(key=lambda x: x[1])
end = intervals[0][1]
count = 1
for i in range(1, len(intervals)):
# Non-overlapping interval found
if intervals[i][0] >= end:
end = intervals[i][1]
count += 1
return len(intervals) - count
7. Divide and Conquer
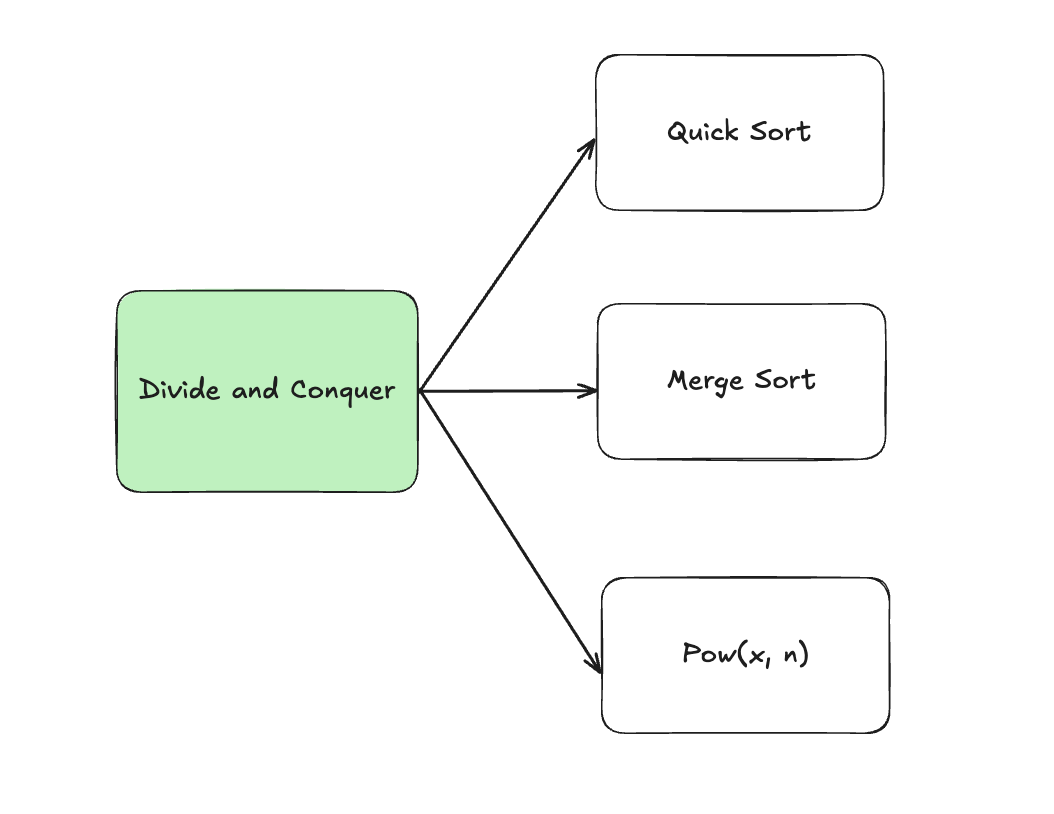
7.1. Merge Sort
-
Step 1: Base case, implement merge_sort_recursive(arr, left, right), merge_two_lists(l1, l2).
-
Step 2: Split Mid => 2 sorted halves, recursion in the same function.
-
Step 3: Merge 2 sorted halves
def merge_two_lists(l1, l2):
result = []
i, j = 0, 0
while i < len(l1) and j < len(l2):
if l1[i] < l2[j]:
result.append(l1[i])
i += 1
else:
result.append(l2[j])
j += 1
result.extend(l1[i:])
result.extend(l2[j:])
return result
def merge_sort_recursive(arr, left, right):
if left == right:
return [arr[left]]
mid = (left + right) // 2
l1 = merge_sort_recursive(arr, left, mid)
l2 = merge_sort_recursive(arr, mid + 1, right)
return merge_two_lists(l1, l2)
def merge_sort(arr):
if not arr:
return []
return merge_sort_recursive(arr, 0, len(arr) - 1)
arr = [1, 7, 4, 1, 10, 9, 2]
print(merge_sort(arr))
7.2. Quick Sort
-
Step 1: Find pivot => implement quick_sort_recursion(arr, left, right) and partition(arr, left, right)
-
Step 2: Init i = start, using j to run (left, right) => if arr[j] <= pivot => Swap arr[j] to left, increase i += 1.
-
Step 3: Final move pivot to the middle.
-
Step 4: Recursive sort for each pivot of subarray (pivot1 of arr1, pivot2 of arr2) => if left < right: => pivot_index = partition(arr, left, right) => quick_sort_recursion(arr, left, pivot_index - 1) => quick_sort_recursion(arr, pivot_index + 1, right)
def partition(arr, left, right):
pivot = arr[right]
i = left - 1
for j in range(left, right):
# Swap to after pivot
# j đi sau i đi trước
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
# Swap pivot
arr[i + 1], arr[right] = arr[right], arr[i + 1]
return i + 1
def quick_sort_recursion(arr, left, right):
if left < right:
pivot_index = partition(arr, left, right)
quick_sort_recursion(arr, left, pivot_index - 1)
quick_sort_recursion(arr, pivot_index + 1, right)
def quick_sort(arr):
quick_sort_recursion(arr, 0, len(arr) - 1)
arr = [1, 7, 4, 1, 10, 9, 2]
quick_sort(arr)
print(arr)
7.3. Pow(x, n)
-
Step 1: Base case
-
Step 2: Divide => Idea: Because in some function, you can not calculate big modular from the start, calculate smaller and merge it.
-
Step 3: Conquer
class Solution:
def myPow(self, x: float, n: int) -> float:
def exponent(base, pow):
# Base case
if pow == 0:
return 1.0
# Divide
half = exponent(base, pow // 2)
# Conquer
if pow % 2 == 0:
return half * half
else:
return half * half * base
if n < 0:
x = 1 / x
n = -n
return exponent(x, n)
8. DFS
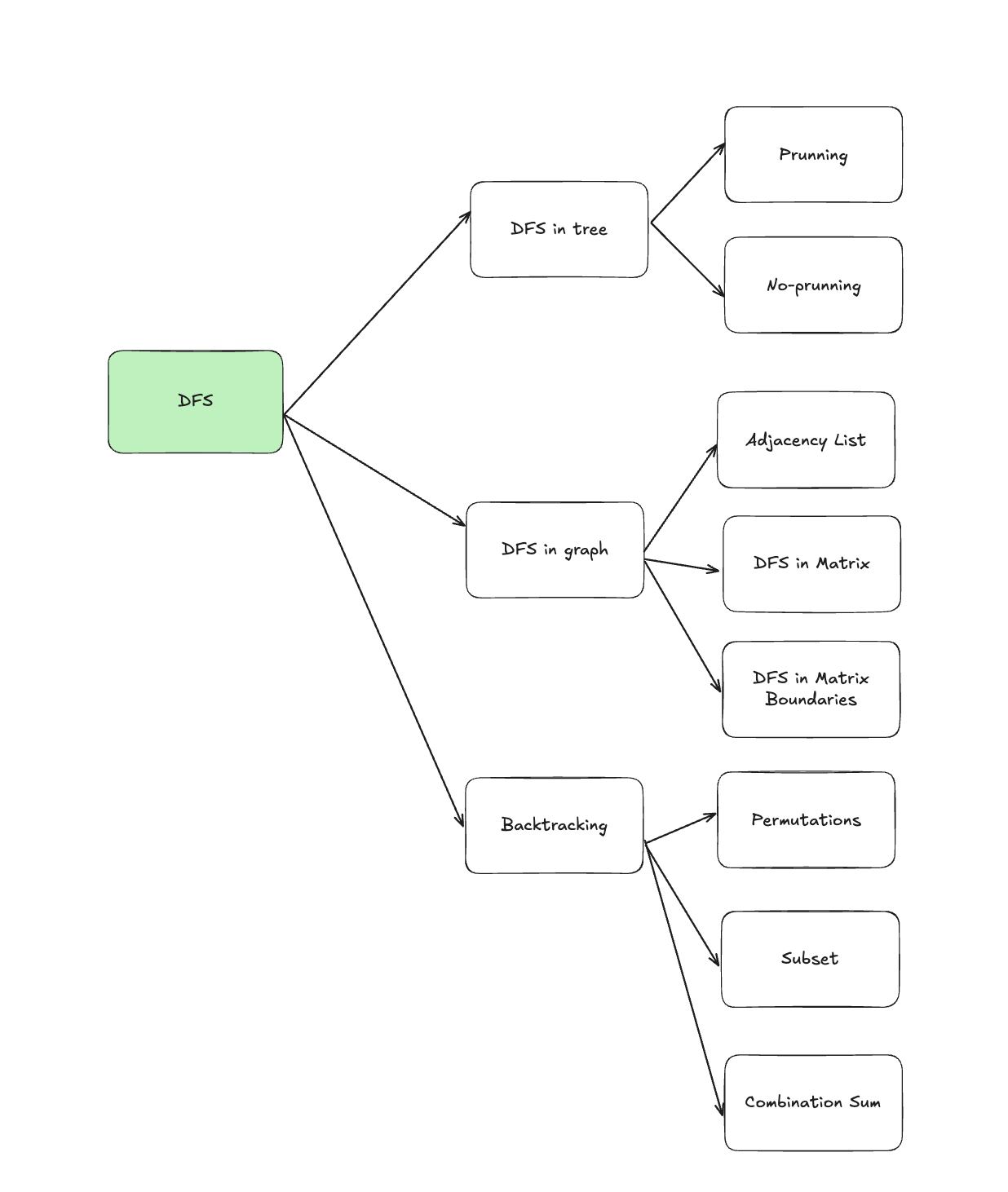
8.1. DFS in tree
8.1.1. Prunning
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: What node.val do
-
Step 4: What left right do
class Solution:
def pathSum(self, nodes: TreeNode, target: int):
def dfs(node, total):
if not node:
return total == target
# Calculate node
total += node.val
# Prunning here
if not node.left and not node.right and total == target:
return True
left = dfs(node.left, total)
right = dfs(node.right, total)
# Left Right trả gì cho root
return left or right
return dfs(nodes, 0)
8.1.2. No-prunning
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: What node.val do
-
Step 4: What left right do
class Solution:
def pathSum(self, root, target):
res = []
def dfs(node, path, curr_sum):
nonlocal res
# Base case
if not node:
return False
# What node do
path.append(node.val)
curr_sum += node.val
if not node.left and not node.right and curr_sum == target:
res.append(path[:])
# Prunning
if curr_sum > target:
return False
# What left and right do
left = dfs(node.left, path, curr_sum)
right = dfs(node.right, path, curr_sum)
# backtrack
path.pop()
return left and right
dfs(root, [], 0)
return res
8.2. DFS in graph
8.2.1. DFS in graph
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
def dfs(adjList):
visited = set()
def dfs_helper(node):
if node in visited:
return
# Visit node
print("Visit node: ", node)
visited.add(node)
for neighbor in adjList[node]:
dfs_helper(neighbor)
# Ensure the unconnected graph is still cover
for node in adjList:
if node not in visited:
dfs_helper(node)
adjList = {
"1": ["2", "4"],
"2": ["1", "3"],
"3": ["2", "4"],
"4": ["1", "3", "5"],
"5": ["4"]
}
dfs(adjList)
8.2.2. Check Cycle
from collections import defaultdict
class Solution:
def graph_valid_tree(self, n, edges):
graph = defaultdict(list)
for start, end in edges:
graph[start].append(end)
graph[end].append(start)
visited = set()
def isCycle(node, parent):
visited.add(node)
for neighbor in graph[node]:
# [0,1] and [1,0] is ok
if neighbor == parent:
continue
# Prunning => True xong không Prunning xuống nữa
if neighbor in visited:
return True
if isCycle(neighbor, node):
return True
return False
# Check not cycle & connected
return not isCycle(0, 0) and len(visited) == n
8.2.3. Matrix: Flood Fill
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
class Solution:
def flood_fill(self, image, sr, sc, color):
m, n = len(image), len(image[0])
# Visited
visited = set()
# Directions
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def dfs(r, c, prev_color, color):
# Base case
if (r, c) in visited:
return
# Prunning
if r < 0 or r >= m or c < 0 or c >= n:
return
if image[r][c] != prev_color or image[r][c] == color:
return
# Node
image[r][c] = color
# Neighbor
for dr, dc in directions:
dfs(r + dr, c + dc, prev_color, color)
dfs(sr, sc, image[sr][sc], color)
return image
8.2.4. Boundaries Matrix: Surrounded Regions
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
Idea:
-
Step 1: DFS in border => ‘O’ to make is ‘S’.
-
Step 2: Change another ‘O’ to ‘X’.
class Solution:
def surrounded_regions(self, grid: List[List[str]]):
if not grid or not grid[0]:
return []
row, col = len(grid), len(grid[0])
visited = set()
# Directions
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def dfs(r, c):
# Base case
if (r, c) in visited:
return
# Prunning
if r < 0 or r >= row or c < 0 or c >= col:
return
if grid[r][c] != 'O':
return
# Node
visited.add((r, c))
grid[r][c] = 'S'
# Check neighbor
for dr, dc in directions:
dfs(r + dr, c + dc)
# Step 1: DFS in col 0 and col - 1
for i in range(row):
if grid[i][0] == 'O':
dfs(i, 0)
if grid[i][col - 1] == 'O':
dfs(i, col - 1)
# Step 2: DFS in row 0 and row - 1
for j in range(col):
if grid[0][j] == 'O':
dfs(0, j)
if grid[row - 1][j] == 'O':
dfs(row - 1, j)
# Step 3: Change another X to O
for i in range(row):
for j in range(col):
if grid[i][j] == 'O':
grid[i][j] = 'X'
elif grid[i][j] == 'S':
grid[i][j] = 'O'
return grid
8.4. Backtracking
8.4.1. Word Search
-
Step 1: Base case
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
-
Step 5: Backtracking out side the directions.
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
row, col = len(board), len(board[0])
visited = set()
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def backtrack(r, c, index):
# Base case
if index == len(word):
return True
# Prunning
if r < 0 or r >= row or c < 0 or c >= col:
return False
if (r, c) in visited:
return False
if board[r][c] != word[index]:
return False
# Node
visited.add((r, c))
index += 1
# Neighbor
for dr, dc in directions:
nr = r + dr
nc = c + dc
if backtrack(nr, nc, index):
return True
visited.remove((r, c))
index -= 1
return False
for i in range(row):
for j in range(col):
if board[i][j] == word[0]:
visited.clear() # Reset after change 'B'
if backtrack(i, j, 0):
return True
return False
8.4.2. Combination
-
Step 1: Base case
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
-
Step 5: Backtrack in loop item.
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
# Subsets = Tree + DFS + Backtrack
phone = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz"
}
result = []
def backtrack(index, path):
# Base case
if index == len(digits):
if path:
result.append(''.join(path[:]))
return
# Prunning
for char in phone[digits[index]]:
# Node
path.append(char)
# Neighbor
backtrack(index + 1, path)
path.pop()
backtrack(0, [])
return result
8.4.3. Subsets
-
Step 1: Base case
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
-
Step 5: Backtrack 2 times => Still index + 1 but not include in path.
class Solution:
def subsets(self, nums: List[int]):
result = []
def backtrack(index, path):
# Base case
if index == len(nums):
result.append(path[:])
return
# Prunning
# Node
path.append(nums[index])
# Neighbor
backtrack(index + 1, path)
# Backtrack
path.pop()
# Magic here
backtrack(index + 1, path)
backtrack(0, [])
return result
8.4.4. Permutations
-
Step 1: Backtrack
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbors
-
Step 5: Backtrack in condition.
class Solution:
def generateParenthesis(self, n: int):
result = []
def backtrack(path, open_bracket, close_bracket):
# Base case
if open_bracket == n and close_bracket == n:
result.append(''.join(path[:]))
return
# Prunning
# Node
if open_bracket < n:
path.append('(')
backtrack(path, open_bracket + 1, close_bracket)
path.pop()
# Neighbors
if close_bracket < open_bracket:
path.append(')')
backtrack(path, open_bracket, close_bracket + 1)
path.pop()
backtrack([], 0, 0)
return result
8.4.5. Combination Sum
-
Step 1: Backtrack
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbors
-
Step 5: Backtrack in loop item.
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
def backtrack(index, path, currSum):
# Base case
if currSum == 0:
result.append(path[:])
return
# Prunning
if index == len(candidates) or currSum < 0:
return
# Neighbor
for i in range(index, len(candidates)):
# Node
path.append(candidates[i])
currSum -= candidates[i]
backtrack(i, path, currSum)
# Backtrack
path.pop()
currSum += candidates[i]
backtrack(0, [], target)
return result
9. BFS
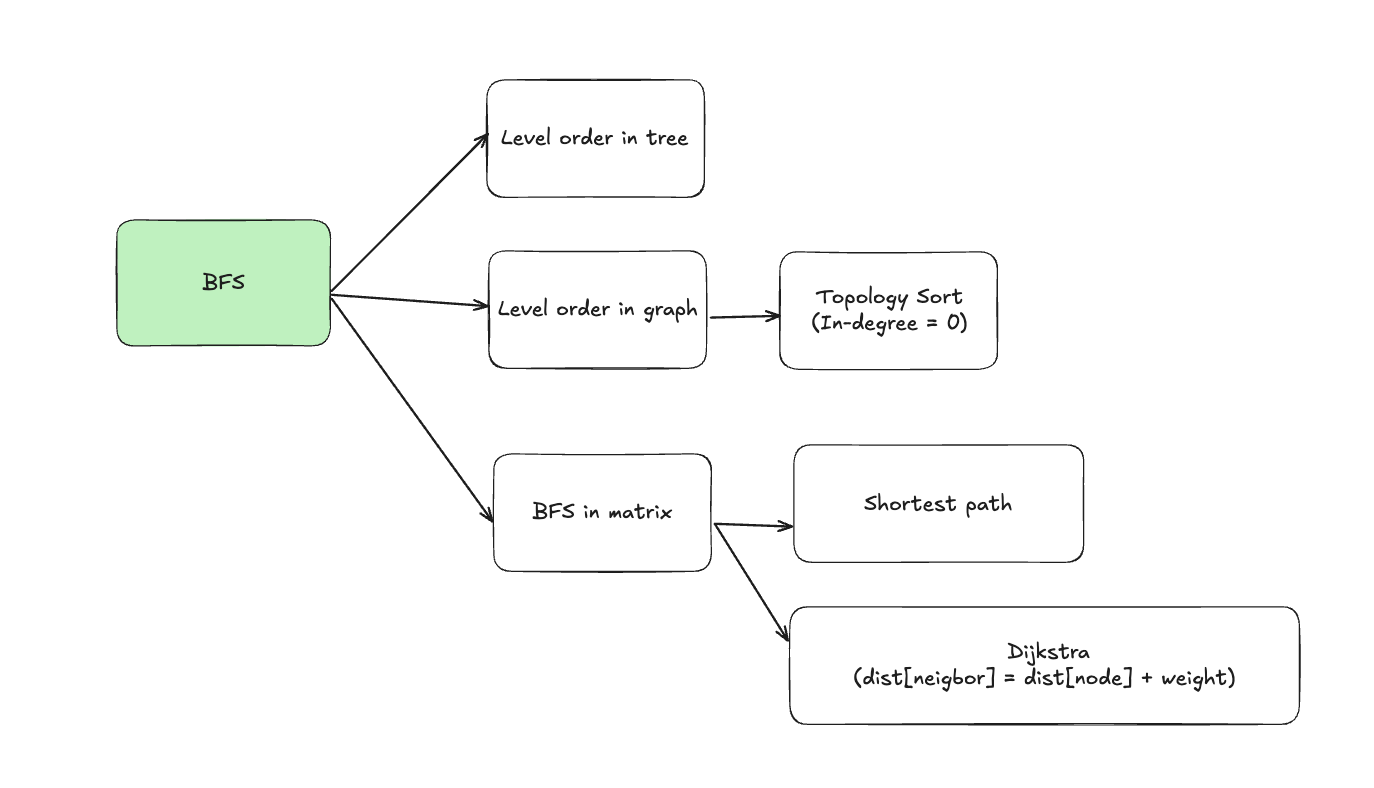
9.1. Level order in tree
-
Step 1: Base case
-
Step 2: Root
-
Step 3: Neighbors
-
Step 4: Level of the queue.
-
Step 5: Pop start
from collections import deque
class Solution:
def level_order_sum(self, root: TreeNode):
# Base case
if not root:
return []
# Root
queue = deque([root])
result = []
# Neighbors
while queue:
# Level Queue
level_size = len(queue)
curr_sum = 0
for _ in range(level_size):
# Pop Start
start = queue.popleft()
curr_sum += start.val
if start.left:
queue.append(start.left)
if start.right:
queue.append(start.right)
result.append(curr_sum)
return result
9.2. Level order in graph
9.2.1. Adjancency List By Level
-
Step 1: Base case
-
Step 2: Visit node
-
Step 3: Visit neighbors
-
Step 4: Level
-
Step 5: Pop left
from collections import deque
def bfs(adjList, root):
# Base case
# Root
visited = set()
queue = deque([root])
# Neighbors
while queue:
# Popleft
start = queue.popleft()
print("Visited:", start)
visited.add(start)
# Neighbors
for neighbor in adjList[start]:
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
adjList = {
"1": ["2", "4"],
"2": ["1", "3"],
"3": ["2", "4"],
"4": ["1", "3", "5"],
"5": ["4"]
}
bfs(adjList, "1")
9.2.2. Matrix Level-By-Level
-
Step 1: Base case
-
Step 2: Visit node
-
Step 3: Visit neighbors
-
Step 4: Level
-
Step 5: Pop left
-
Step 6: Neighbors
-
Step 7: Prunning
-
Step 8: Visit neighbors
Notes: queue = deque([(r, c)]): The way to init a tuple
from collections import deque
def bfs(grid, r, c):
# Base case
# Node
visited = set()
# The way to init a tuple
queue = deque([(r, c)])
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
result = []
# Neighbors
while queue:
level_size = len(queue)
temp = []
for _ in range(level_size):
# Pop left
start_row, start_col = queue.popleft()
visited.add((start_row, start_col))
temp.append((start_row, start_col))
# Visited the neighbors
for dr, dc in directions:
n_row = start_row + dr
n_col = start_col + dc
# Prunning
if n_row < 0 or n_row >= len(grid) or n_col < 0 or n_col >= len(grid[0]):
continue
if (n_row, n_col) in visited:
continue
queue.append((n_row, n_col))
visited.add((n_row, n_col))
result.append(temp)
return result
matrix = [
[0, 0, 0],
[0, 1, 1],
[0, 1, 0]
]
print(bfs(matrix, 0, 0))
9.4. Shortest path
- Idea: it is a level of the graph.
from collections import defaultdict
from collections import deque
class Solution:
def bus_routes(self, routes: List[List[int]], source: int, target: int):
# Init
graph = defaultdict(list)
for route in routes:
n = len(route)
for i in range(n):
for j in range(n):
if route[i] != route[j] and route[j] not in graph[route[i]]:
graph[route[i]].append(route[j])
# Node
visited = set()
queue = deque([source])
count = 0
# Neighbor
while queue:
# Level
level_size = len(queue)
for _ in range(level_size):
# Pop left
start = queue.popleft()
if start == target:
return count
for neighbor in graph[start]:
# Prunning
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
count += 1
return -1
9.5. BFS in multiple start points
- Idea: BFS in multiple start points.
from collections import deque
class Solution:
def rotting_oranges(self, grid: List[List[str]]):
if not grid or not grid[0]:
return -1
row, col = len(grid), len(grid[0])
fresh_oranges = 0
# Node
visited = set()
queue = deque()
times = -1
for i in range(row):
for j in range(col):
if grid[i][j] == 'R':
queue.append((i, j))
visited.add((i, j))
elif grid[i][j] == 'F':
fresh_oranges += 1
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
# Neighbors
while queue:
# Level (Count)
level_size = len(queue)
for _ in range(level_size):
# Pop left
start_row, start_col = queue.popleft()
# Neighbors
for dr, dc in directions:
n_row = start_row + dr
n_col = start_col + dc
# Prunning
if n_row < 0 or n_row >= row or n_col < 0 or n_col >= col:
continue
if (n_row, n_col) in visited:
continue
if grid[n_row][n_col] != 'F':
continue
grid[n_row][n_col] = 'R'
queue.append((n_row, n_col))
visited.add((n_row, n_col))
fresh_oranges -= 1
times += 1
return times if fresh_oranges == 0 else -1
9.5. Topology Sort
Notes: Không phải visited mà indegree[i] = 0
-
Step 1: Build Indegree
-
Step 2: Add indegree = 0 to queue
-
Step 3: Node
-
Step 4: Neighbor, indegree -= 1, add indegree = 0 to queue
-
Step 5: Popleft
from collections import defaultdict, deque
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]):
# Indegree
in_degrees = [0] * numCourses
# Adjancy List
adj_list = defaultdict(list)
for u, v in prerequisites:
in_degrees[v] += 1
adj_list[u].append(v)
# Node
queue = deque([u for u in range(numCourses) if in_degrees[u] == 0])
result = []
# Neighbor
while queue:
# Popleft
start = queue.popleft()
result.append(start)
for neighbor in adj_list[start]:
in_degrees[neighbor] -= 1
if in_degrees[neighbor] == 0:
queue.append(neighbor)
return len(result) == numCourses
9.6. Dijkstra
Dijkstra = BFS + thay deque to heapq + dist[i] to store start -> i => dist[neighbor] = dist[start] + weight
-
Step 1: Init pq = [(0, start)], dist[start] = 0
-
Step 2: Node
-
Step 3: Neighbor
-
Step 4: Update min distance to start -> i -> j -> end, push when dist[neighbor] = dist[start] + weight => Push neighbor to heap to continue calculate heapq.heappush(pq, (dist[neighbor], neighbor))
import heapq
from collections import defaultdict
def dijkstra(graph, start):
# Init heap
dist = defaultdict(lambda: float('inf'))
# Node
pq = [(0, start)] # dist[start -> start] = 0
dist[start] = 0
# Neighbor
while pq:
curr_dist, start = heapq.heappop(pq)
# Prunning
if curr_dist > dist[start]:
continue
# Dist
for neighbor, weight in graph[start]:
if dist[neighbor] > dist[start] + weight:
dist[neighbor] = dist[start] + weight
heapq.heappush(pq, (dist[neighbor], neighbor))
return dist
graph = {
'A': [('B', 5), ('C', 1)],
'B': [('A', 5), ('C', 2), ('D', 1)],
'C': [('A', 1), ('B', 2), ('D', 4), ('E', 8)],
'D': [('B', 1), ('C', 4), ('E', 3), ('F', 6)],
'E': [('C', 8), ('D', 3)],
'F': [('D', 6)]
}
start_node = 'A'
distances = dijkstra(graph, start_node)
for node in sorted(distances):
print(f"Distance from {start_node} to {node}: {distances[node]}")
10. Greedy
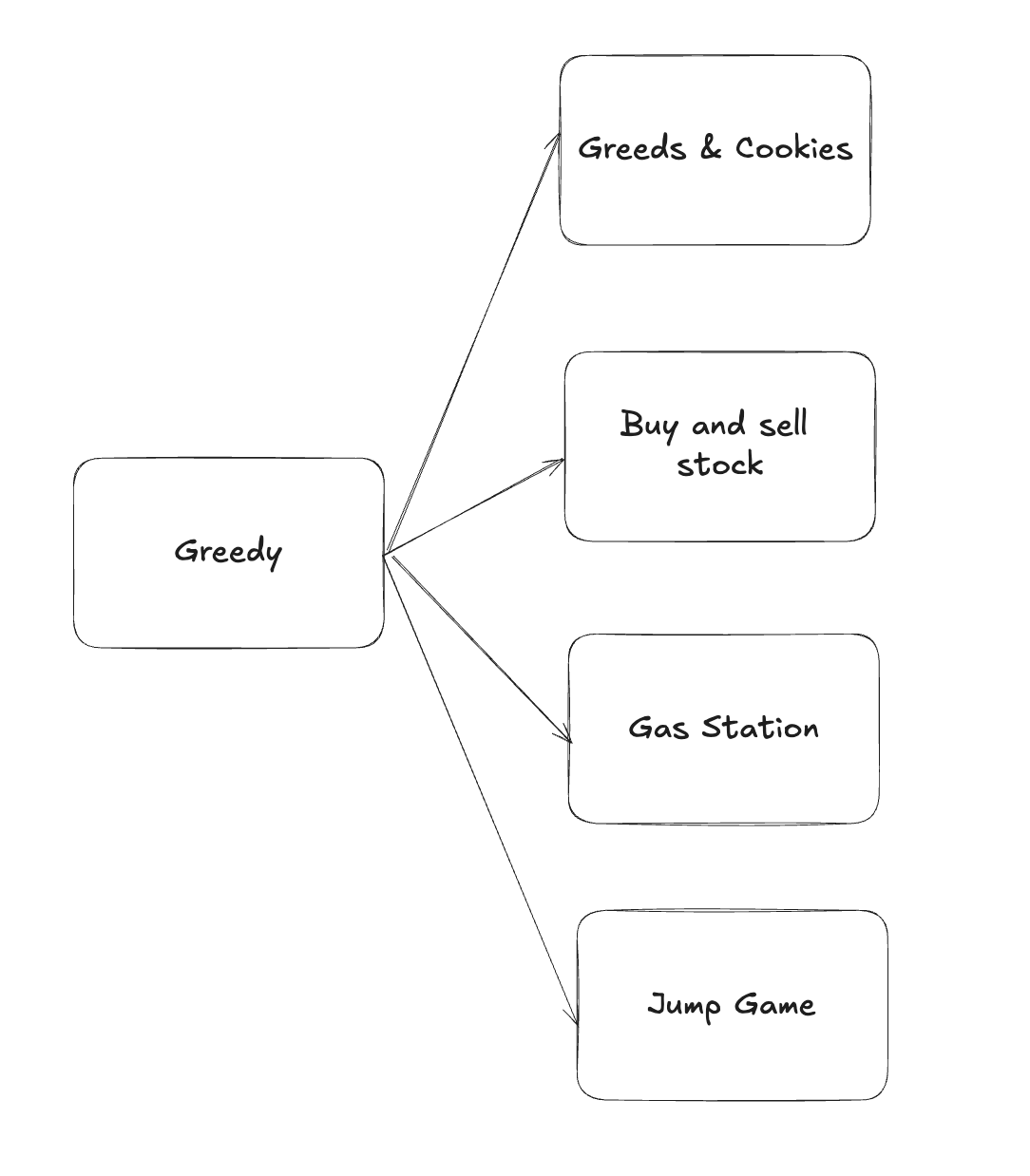
10.1. Greeds & Cookies
-
Step 1: Init i, j.
-
Step 2: If cookies[j] >= greeds[i] => increase i += 1.
-
Step 3: Only increase j.
-
Step 4: Return count.
def findContentChildren(greeds, cookies):
greeds.sort()
cookies.sort()
count = 0
i, j = 0, 0
while i < len(greeds) and j < len(cookies):
# current cookie can satisfy current child
if cookies[j] >= greeds[i]:
count += 1
i += 1
j += 1
return count
10.2. Buy and sell stock
-
Step 1: Loop in prices
-
Step 2: Update min_price.
-
Step 3: Calculate the max_profit.
def maxProfit(prices):
if not prices:
return 0
min_price = prices[0]
max_profit = 0
for price in prices:
min_price = min(min_price, price)
max_profit = max(max_profit, price - min_price)
return max_profit
10.3. Gas Station
-
Step 1: Loop each item.
-
Step 2: If do not have enough cost for fuel => Go to the next station.
-
Step 3: Else fill the fuel and spend cost go to the next station.
def canCompleteCircuit(gas, cost):
if sum(gas) < sum(cost):
return -1
start, fuel = 0, 0
for i in range(len(gas)):
if fuel + gas[i] - cost[i] < 0:
# can't reach next station:
# try starting from next station
start, fuel = i + 1, 0
else:
# can reach next station:
# update remaining fuel
fuel += gas[i] - cost[i]
return start
10.4. Jump Game
-
Step 1: Loop i item in array.
-
Step 2: max_reach = max(max_reach, i + nums[i])
class Solution:
def canJump(self, nums: List[int]):
max_reach = 0
for i in range(len(nums)):
if i > max_reach:
return False
max_reach = max(max_reach, i + nums[i])
return True
11. Bit Manipulation
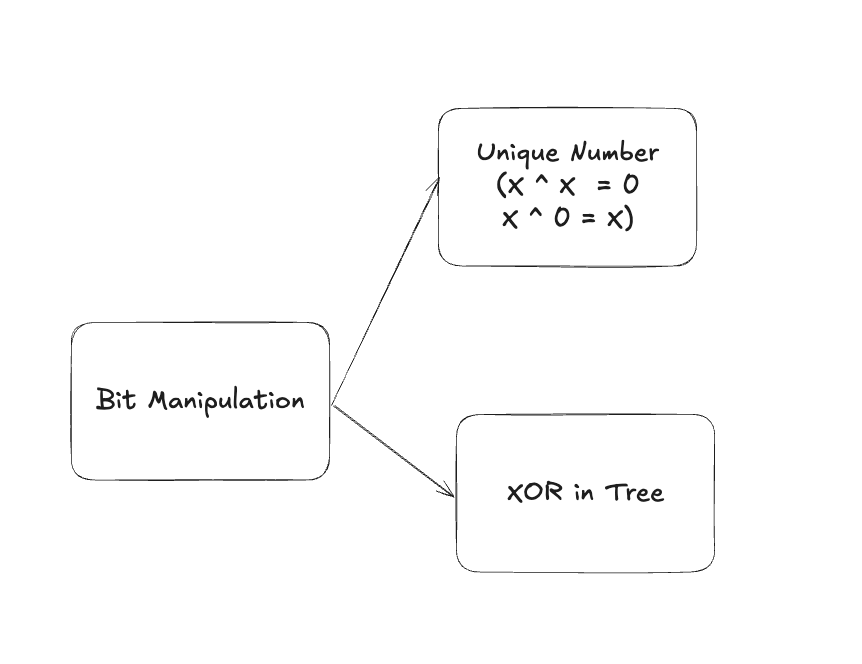
11.1. Find the missing number
-
Step 1: XOR full.
-
Step 2: XOR num in array.
-
Step 3: XOR xor_full & xor_array
def find_missing_number(nums, n):
xor_full = 0
xor_array = 0
# XOR all numbers from 1 to n
for i in range(1, n + 1):
xor_full ^= i
# XOR all elements in the array
for num in nums:
xor_array ^= num
# Missing number is the difference of the two XORs
return xor_full ^ xor_array
# Example usage:
nums = [1, 2, 4, 5, 6] # Missing number is 3
n = 6
missing = find_missing_number(nums, n)
print("Missing number is:", missing)
11.2. XOR in binary tree
Idea recursion: Hiện tại ở node left -> chỉ nhìn 2 thằng con của nó thôi => abstract lên.
-
Step 1: XOR the left node => store value.
-
Step 2: XOR the right node => store value.
-
Step 3: XOR the root node => left _ right _ root.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def xor_subtree(node):
if not node:
return 0
# Recursively compute XOR of left and right subtrees
left_xor = xor_subtree(node.left)
right_xor = xor_subtree(node.right)
# Update current node's value
node.val = node.val ^ left_xor ^ right_xor
# Return total XOR of this subtree to parent
return node.val
# Build the tree
root = TreeNode(5)
root.left = TreeNode(3)
root.right = TreeNode(8)
root.left.left = TreeNode(1)
root.left.right = TreeNode(4)
# Apply XOR transformation
xor_subtree(root)
# Print the transformed tree (in-order)
def print_inorder(node):
if node:
print_inorder(node.left)
print(node.val, end=" ")
print_inorder(node.right)
print("Tree after XOR transformation (in-order):")
print_inorder(root)
12. Trie
12.1. Implement
It is Kth Tree Problem.
-
Step 1: Nth Tree => not binary tree
-
Step 2: Insert/Update/Delete still O(L)
-
Step 3: Insert => Loop char in word => If char not in children => node.children[char] = TrieNode() => Else: node = node.children[char] => Out loop and node.isEndOfWord = True
-
Step 4: Search => Loop char in word => If char not in children => Return False => Else: node = node.children[char] => Out loop and node.isEndOfWord = True => Return True.
-
Step 5: Delete
Process: Kth Tree
- Step 1: Loop in node.children
- Step 2: Base case.
- Step 3: Prunning.
- Step 4: Node.
- Step 5: Neighbors.
- Step 6: Backtrack delete.
class TrieNode:
def __init__(self):
self.children = {}
self.isEndOfWord = False
class Solution:
def create_trie(self, words):
# === DO NOT MODIFY ===
self.root = TrieNode()
for word in words:
self.insert(word)
def insert(self, word):
# === DO NOT MODIFY ===
node = self.root
for char in word:
if char not in node.children:
node.children[char] = TrieNode()
node = node.children[char]
node.isEndOfWord = True
def search(self, word):
"""
Search the trie for the given word.
Returns True if the word exists in the trie, False otherwise
"""
node = self.root
for char in word:
if char not in node.children:
return False
node = node.children[char]
return node.isEndOfWord
def delete(self, word):
def dfs_helper(node, index):
# Base case
if index == len(word):
if not node.isEndOfWord:
return False
node.isEndOfWord = False
return len(node.children) == 0
# Node
child = node.children.get(word[index])
# Prunning
if not child:
return False
# Neighbor
should_deleted = dfs_helper(child, index + 1)
# Backtrack
if should_deleted:
del node.children[word[index]]
return not node.isEndOfWord and len(node.children) == 0
dfs_helper(self.root, 0)
def trie(self, initialWords, commands):
# === DO NOT MODIFY ===
self.create_trie(initialWords)
output = []
for command, word in commands:
if command == "search":
output.append(self.search(word))
elif command == "delete":
self.delete(word)
return output
12.2. Prefix Matching:
-
Step 1: Loop char in word.
-
Step 2: Go to the last prefix.
-
Step 3: DFS for the final word
-
Step 4: Key is char, Value is children.
for char, child in node.children.items()
class TrieNode:
def __init__(self):
self.children = {}
self.isEndOfWord = False
class Solution:
def create_trie(self, words):
# === DO NOT MODIFY ===
self.root = TrieNode()
for word in words:
self.insert(word)
def insert(self, word):
# === DO NOT MODIFY ===
node = self.root
for char in word:
if char not in node.children:
node.children[char] = TrieNode()
node = node.children[char]
node.isEndOfWord = True
def prefix(self, word):
"""
Return a list of all words in the trie that start with the given prefix.
"""
# Step 1: Go to the last prefix
node = self.root
for char in word:
if char not in node.children:
return []
node = node.children[char]
# Step 2: DFS for the final word
res = []
def dfs(node, path):
# Base case
if node.isEndOfWord:
res.append(''.join(path[:]))
if len(node.children) == 0:
return
# Node
for char, child in node.children.items():
path.append(char)
dfs(child, path)
path.pop()
dfs(node, list(word))
return res
def trie(self, words, prefix):
# === DO NOT MODIFY ===
self.create_trie(words)
return self.prefix(prefix)
13. Dynamic Programming
13.1. Bounded Knapstack
-
Step 1: Create a (n + 1) x (capacity + 1) matrix.
-
Step 2: If weight > capacity => No get it.
-
Step 3: Else => Get or not get.
dp[i][j] = max(
dp[i - 1][j], # Don't take item i
dp[i - 1][j - weights[i - 1]] + values[i - 1] # Take item i once
)
def knapsack(weights, values, capacity):
# Create 2-D dp array to carry i item with capacity
n = len(values)
dp = [[0] * (capacity + 1) for _ in range(n + 1)]
# Loop and update array
for i in range(1, n + 1):
for j in range(capacity + 1):
if weights[i - 1] > j:
dp[i][j] = dp[i - 1][j]
else:
# Lay hoac khong lay item i
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])
return dp[n][capacity]
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 5
print(knapsack(weights, values, capacity))
13.2. Total Sum
-
Step 1: Create a [target + 1] matrix => 1 state.
-
Step 2: Loop for num in nums
-
Step 3: dp[j] = dp[j] + dp[j - num]
from typing import List
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
total = sum(nums)
if (total + target) % 2 != 0 or abs(target) > total:
return 0
target_sum = (total + target) // 2
n = len(nums)
# dp[i][j] = number of ways to reach sum j using first i numbers
dp = [[0] * (target_sum + 1) for _ in range(n + 1)]
dp[0][0] = 1 # One way to reach sum 0 with 0 elements
for i in range(1, n + 1):
num = nums[i - 1]
for j in range(target_sum + 1):
if j < num:
dp[i][j] = dp[i - 1][j] # can't pick num
else:
# Pick num or skip it
dp[i][j] = dp[i - 1][j] + dp[i - 1][j - num]
return dp[n][target_sum]
13.3. Unbounded Knapstack
dp[i][j] = max(
dp[i - 1][j], # Don't take item i
dp[i][j - weights[i - 1]] + values[i - 1] # Take item i, and possibly take it again
)
def unbounded_knapsack_2d(weights, values, capacity):
n = len(weights)
dp = [[0] * (capacity + 1) for _ in range(n + 1)]
for i in range(1, n + 1): # i = item index (1-based)
for w in range(capacity + 1): # w = current capacity
if weights[i - 1] <= w:
# Option 1: take current item (stay at i)
# Option 2: don't take current item (move to i-1)
dp[i][w] = max(dp[i - 1][w], dp[i][w - weights[i - 1]] + values[i - 1])
else:
# Cannot take current item
dp[i][w] = dp[i - 1][w]
return dp[n][capacity]
# Example usage
weights = [2, 3, 4]
values = [40, 50, 100]
capacity = 8
print(unbounded_knapsack_2d(weights, values, capacity)) # Output: 200
13.4. Coin Change Value
-
Step 1: Loop to i.
-
Step 2: Loop to target.
-
Step 3: If allow dup => get from dp[i][target], else if get not dup => dp[i - 1][target].
from typing import List
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
n = len(coins)
INF = float('inf')
# dp[i][j] = min coins needed to make sum j using first i coins
dp = [[INF] * (amount + 1) for _ in range(n + 1)]
for i in range(n + 1):
dp[i][0] = 0 # 0 coins needed to make sum 0
for i in range(1, n + 1):
coin = coins[i - 1]
for j in range(amount + 1):
if j < coin:
dp[i][j] = dp[i - 1][j] # can't use this coin
else:
# Option 1: don't use the coin (dp[i-1][j])
# Option 2: use the coin (stay at i for unbounded)
dp[i][j] = min(dp[i - 1][j], dp[i][j - coin] + 1)
return dp[n][amount] if dp[n][amount] != INF else -1
13.5. Coin Change Way to Pick (Biến cố độc lập)
from typing import List
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
n = len(coins)
# dp[i][j] = number of ways to make sum j using first i coins
dp = [[0] * (amount + 1) for _ in range(n + 1)]
# Base case: 1 way to make amount 0 (pick nothing)
for i in range(n + 1):
dp[i][0] = 1
for i in range(1, n + 1):
coin = coins[i - 1]
for j in range(amount + 1):
if j < coin:
dp[i][j] = dp[i - 1][j] # can't use coin
else:
# Option 1: don't use this coin (dp[i-1][j])
# Option 2: use this coin (stay at i, subtract value)
dp[i][j] = dp[i - 1][j] + dp[i][j - coin]
return dp[n][amount]
13.7. Subsequence (Biến cố phụ thuộc)
-
Step 1: Loop to i.
-
Step 2: Loop to target.
-
Step 3: If common character => dp[i][j] = dp[i - 1][j - 1] + 1
-
Step 4: If not => Skip i or skip j => max(dp[i - 1][j], dp[i][j - 1])
class Solution:
def longestCommonSubsequence(self, s1: str, s2: str) -> int:
m, n = len(s1), len(s2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if s1[i - 1] == s2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[m][n]
13.8. Palindrome
-
Step 1: Loop to i.
-
Step 2: Loop to target.
-
Step 3: If common character => dp[i][j] = 2 + dp[i + 1][j - 1]
-
Step 4: If not => Skip i or skip j => dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
Notes:
Because: it depend on dp[i + 1][j - 1], dp[i + 1][j], dp[i][j - 1]
-
Case 1: s[i] == s[j]. If the two ends match, they can be part of the palindrome, so we include them and look inside: from i+1 to j-1.
-
Case 2: In s[i+1..j] (skip s[i]). Or in s[i..j-1] (skip s[j])
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
# Create a 2D DP array initialized to 0
dp = [[0] * n for _ in range(n)]
# Base case: single characters are palindromes of length 1
for i in range(n):
dp[i][i] = 1
# Fill the DP table
for i in range(n - 1, -1, -1): # i goes from n-1 to 0
for j in range(i + 1, n): # j goes from i+1 to n-1
if s[i] == s[j]:
dp[i][j] = 2 + dp[i + 1][j - 1]
else:
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
return dp[0][n - 1]
13.9. Robot Matrix
-
Step 1: Fill top and left.
-
Step 2: Come from left or top => dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
class Solution:
def unique_paths(self, m: int, n: int) -> int:
# Initialize a 2D array with dimensions m x n
dp = [[0] * n for _ in range(m)]
# base case: there is only one way to reach any cell in the first row (moving only right)
for i in range(n):
dp[0][i] = 1
# Set base case: there is only one way to reach any cell in the first column (moving only down)
for j in range(m):
dp[j][0] = 1
# Fill the rest of the dp array
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
13.10. Maximum Profit Scheduling
-
Step 1: Sort by start_time.
-
Step 2: Find the next job after end.
-
Step 3: dp[i] = max(dp[i - 1], dp[idx] + p)
from bisect import bisect_right
from typing import List
class Solution:
def job_scheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
# Sort jobs by end time
jobs = sorted(zip(startTime, endTime, profit), key=lambda x: x[1])
# Extract end times for binary search
ends = [job[1] for job in jobs]
dp = [0] * (len(jobs) + 1)
for i in range(1, len(jobs) + 1):
start, end, p = jobs[i - 1]
idx = bisect_right(ends, start)
dp[i] = max(dp[i - 1], dp[idx] + p)
return dp[-1]
13.11. Edit Distance
-
Step 1: dp[i][0] = i => Convert word i to the word2[j] with 0 characters
-
Step 2: dp[0][j] = i => Convert word i to the word2[j] with j characters
-
Step 3: if word1[i - 1] == word2[j - 1] => Do not do anything.
-
Step 4: Else => Insert, Delete, Replace
dp[i][j] = 1 + min(
dp[i - 1][j], # delete
dp[i][j - 1], # insert
dp[i - 1][j - 1] # replace
)
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
m, n = len(word1), len(word2)
# dp[i][j] = min operations to convert word1[0..i-1] to word2[0..j-1]
dp = [[0] * (n + 1) for _ in range(m + 1)]
# Initialize base cases
for i in range(m + 1):
dp[i][0] = i # delete all characters
for j in range(n + 1):
dp[0][j] = j # insert all characters
# Fill DP table
for i in range(1, m + 1):
for j in range(1, n + 1):
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] # no operation needed
else:
dp[i][j] = 1 + min(
dp[i - 1][j], # delete
dp[i][j - 1], # insert
dp[i - 1][j - 1] # replace
)
return dp[m][n]
13.12. Robber House
- Top-down:
def rob(treasure):
if not treasure:
return 0
def rob_helper(i):
# Base case
if i == 0:
return 0
if i == 1:
return treasure[0]
# Node
take = rob_helper(i - 2) + treasure[i - 1]
skip = rob_helper(i - 1)
# Result
return max(take, skip)
n = len(treasure)
return rob_helper(n)
treasure = [2, 7, 9, 3, 1]
print(rob(treasure)) # Output: 12
- Memoization:
- Add memo to store the current result => memo = {} => if i in memo => return memo[i] => memo[i] = max(take, skip)
def rob(treasure):
if not treasure:
return 0
memo = {}
def rob_helper(i):
# Base case
if i == 0:
return 0
if i == 1:
return treasure[0]
# Memoization
if i in memo:
return memo[i]
# Node
take = rob_helper(i - 2) + treasure[i - 1]
skip = rob_helper(i - 1)
memo[i] = max(take, skip)
# Result
return memo[i]
n = len(treasure)
return rob_helper(n)
treasure = [2, 7, 9, 3, 1]
print(rob(treasure)) # Output: 12
- Bottom-up:
-
Covert memoization table in top-down to bottom-up.
-
Store data with (n + 1) elements
Step 1: Init dp tables.
Step 2: Base case for start calculate.
Step 3: Calculate.
def rob(treasure):
if not treasure:
return 0
# Init dp table
n = len(treasure)
dp = [0] * (n + 1)
# Base case
dp[0] = 0
dp[1] = treasure[0]
for i in range(2, n + 1):
# Calculate
dp[i] = max(dp[i - 1], dp[i - 2] + treasure[i - 1])
return dp[n]
treasure = [2, 7, 9, 3, 1]
print(rob(treasure)) # Output: 12
14. Prefix Sum
14.1. Count Vowels in Substrings
class Solution:
def vowelStrings(self, word: str, queries: List[List[int]]):
vowels = 'aoeui'
n = len(word)
prefix = [0] * (n + 1)
# Start from i = 1 to use prefix[i - 1]
for i in range(1, n + 1):
prefix[i] = prefix[i - 1] + (1 if word[i - 1] in vowels else 0)
result = []
for start, end in queries:
result.append(prefix[end + 1] - prefix[start])
return result
14.2. Subarray Sum Equals K
Step 1: Find subarray.
Step 2: Find [i, j] where prefix[j] - prefix[i] = k
class Solution:
def subarraySum(self, nums: List[int], k: int) -> int:
prefix_sum = 0
count = 0
sum_count = {0: 1} # Initialize with 0 sum having 1 count
for num in nums:
prefix_sum += num
# If (prefix_sum - k) exists in sum_count, it means we found subarrays summing to k
if prefix_sum - k in sum_count:
count += sum_count[prefix_sum - k]
# Update the count of current prefix sum
sum_count[prefix_sum] = sum_count.get(prefix_sum, 0) + 1
return count
15. Matrix
15.1. Spiral Matrix
Step 1: Top Row
Step 2: Right Column
Step 3: Bottom Row
Step 4: Left Column
class Solution:
def spiral_order(self, matrix: List[List[int]]):
result = []
while matrix:
result += matrix.pop(0)
if matrix and matrix[0]:
for row in matrix:
result.append(row.pop())
if matrix:
result += matrix.pop()[::-1]
if matrix and matrix[0]:
for row in matrix[::-1]:
result.append(row.pop(0))
return result
15.2. Rotate Image
class Solution:
def rotate_image(self, matrix: List[List[int]]):
n = len(matrix)
# Transpose the matrix
for i in range(n):
for j in range(i, n):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
# Reverse each row
for i in range(n):
matrix[i] = matrix[i][::-1]
return matrix
15.3. Set Matrix Zeroes
def setZeroes(matrix):
rows, cols = len(matrix), len(matrix[0])
zero_rows, zero_cols = set(), set()
for i in range(rows):
for j in range(cols):
if matrix[i][j] == 0:
zero_rows.add(i)
zero_cols.add(j)
for row in zero_rows:
for col in range(cols):
matrix[row][col] = 0
for col in zero_cols:
for row in range(rows):
matrix[row][col] = 0
return matrix
