Framework Thinking - Neetcode 150 - Combination Sum 2
Here is solutions for Combination Sum 2.
1. Understand the problem
-
You are given:
-
candidates[]: can contains duplicate
-
target: integer
-
-
Return all unique combinations where sum = target, each number can only used once, and no duplicate combinations.
2. Clarify constraints, asks 4 - 5 questions including edge cases.
- Can I reuse the element ?
- Can not reuse the element.
- Can candidates contain duplicates ?
- Yes
- Can the result contain duplicate combinations ?
- No
- Does order matter ?
- No [1, 7] is same [7, 1]
- What if no combination exists ?
- Return empty list []
3. Explore examples.
Example 1:
candidates = [10,1,2,7,6,1,5]
target = 8
Output:
[1,1,6], [1,2,5], [1,7], [2,6]
4. Brainstorm 2 - 3 solutions, naive solution first and optimize later. Explain the key idea of each solution.
4.1. Naive Backtracking - Time O(2^N), Space: O(2^n)
-
Idea: Do not O(2^N * N) due to each element picked only once.
-
Using a set to store the result.
-
Time: O(2^N)
-
Space: O(2^N)
4.2. Optimized Backtracking with Prunning - Time O(2^N), Space O(2^n)
-
Idea: Sort it first, and prunning if candidates[i] == candidates[i - 1] and i > n.
-
Time: O(2^N)
-
Space: O(2^n)
5. Implement solutions.
5.1. Naive Backtracking - Time O(N * 2^N), Space O(N * 2^N)
class Solution:
def combinationSum2(self, candidates, target):
res = set()
candidates.sort()
def generate_subsets(i, cur, total):
if total == target:
res.add(tuple(cur))
return
if total > target or i == len(candidates):
return
cur.append(candidates[i])
generate_subsets(i + 1, cur, total + candidates[i])
cur.pop()
generate_subsets(i + 1, cur, total)
generate_subsets(0, [], 0)
return [set(combination) for combination in res]
-
Time: O(N * 2^N).
-
Space: O(N * 2^N)
5.2. Backtracking with Prunning - Time O(N * 2^N), Space O(N)
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
candidates.sort()
def dfs(i, cur, total):
if total == target:
res.append(cur.copy())
return
if total > target or i == len(candidates):
return
# Case 1: Get this value
cur.append(candidates[i])
dfs(i + 1, cur, total + candidates[i])
cur.pop()
# Case 2: Skip duplicate values
while i + 1 < len(candidates) and candidates[i] == candidates[i+1]:
i += 1
dfs(i + 1, cur, total)
dfs(0, [], 0)
return res
- Idea:
# Skip duplicate values
while i + 1 < len(candidates) and candidates[i] == candidates[i+1]:
i += 1
This loop ensures:
- When we skip a number, we also skip all its duplicates
- So we only skip one "group" of equal values
- If you have [1,1,2,2] => You still pick the duplicate 1 in the pick branch, only skip the skip branch => So you do not pick (1-a,1-b, 2,3) and (1-b, 1-a, 2, 3)
-
Time: O(N * 2^N).
-
Space: O(N)
5.3. Naive Backtracking with Hash - Time O(N * 2^N), Space O(N)
class Solution:
def combinationSum2(self, nums, target):
self.res = []
self.count = defaultdict(int)
cur = []
A = []
for num in nums:
if self.count[num] == 0:
A.append(num)
self.count[num] += 1
self.backtrack(A, target, cur, 0)
return self.res
def backtrack(self, nums, target, cur, i):
if target == 0:
self.res.append(cur.copy())
return
if target < 0 or i >= len(nums):
return
if self.count[nums[i]] > 0:
cur.append(nums[i])
self.count[nums[i]] -= 1
self.backtrack(nums, target - nums[i], cur, i)
self.count[nums[i]] += 1
cur.pop()
self.backtrack(nums, target, cur, i + 1)
-
Time: O(N * 2^N).
-
Space: O(N)
5.4. Optimize Prunning - Time O(N * 2^N), Space O(N)
Idea:
- If you have [1,1,2,2] => You still pick the duplicate 1 in the pick branch, only skip the skip branch => So you do not pick (1-a,1-b, 2,3) and (1-b, 1-a, 2, 3)
class Solution:
def combinationSum2(self, candidates: List[int], target: int) -> List[List[int]]:
res = []
candidates.sort()
def dfs(idx, path, cur):
if cur == target:
res.append(path.copy())
return
for i in range(idx, len(candidates)):
if i > idx and candidates[i] == candidates[i - 1]:
continue
if cur + candidates[i] > target:
break
path.append(candidates[i])
dfs(i + 1, path, cur + candidates[i])
path.pop()
dfs(0, [], 0)
return res
-
Time: O(N * 2^N).
-
Space: O(N)
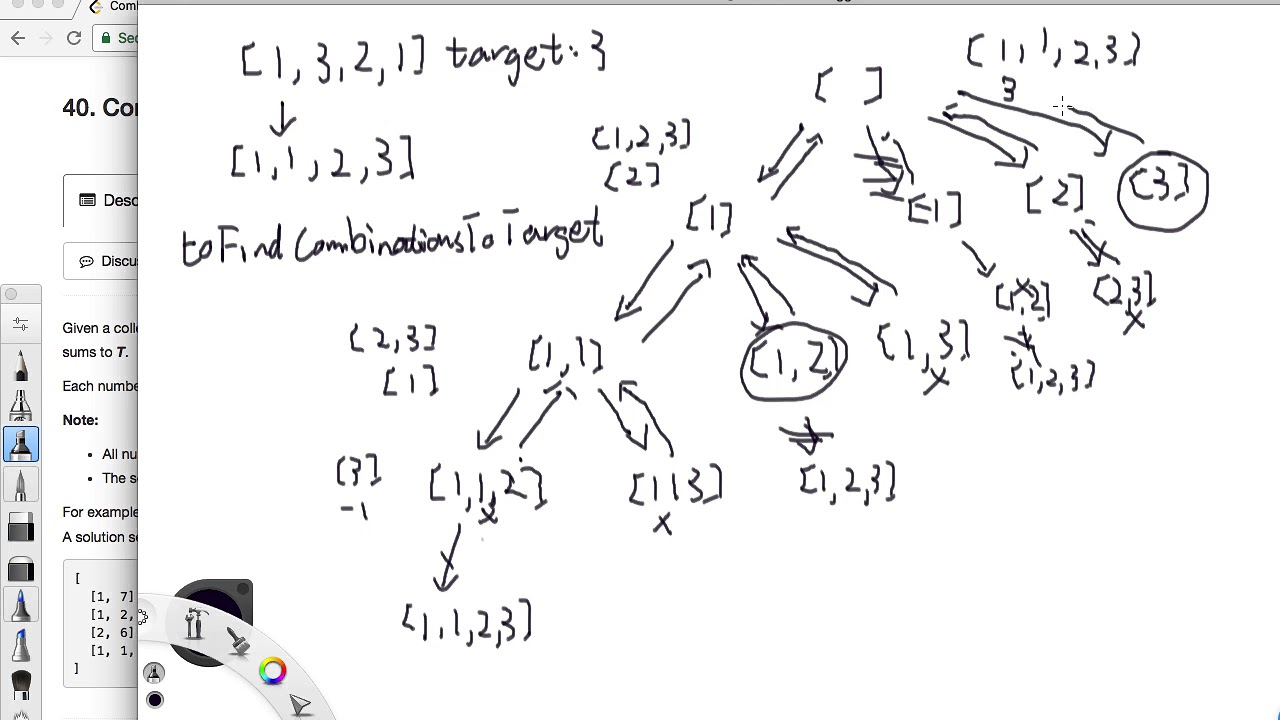
6. Dry run testcases.
December 5, 2025
