Here is solutions for Combination Sum.

1. Understand the problem

• You are given:

  • An array of distinct positive integers candidates

  • A target integer target

• Your task is to return all unique combinations of candidates where the chosen numbers sum to target.

2. Clarify constraints, asks 4 - 5 questions including edge cases.

1. Are all numbers positive?

• Yes (important to avoid infinite loops)

1. Can candidates contain duplicates?

• No (distinct integers)

1. Can I reuse the same number multiple times?

• Yes (unlimited usage)

1. What should I return if no combination exists?

• Return an empty list []

1. What about edge cases like an empty candidates list or target = 0?

• candidates = [] → return []

• target = 0 → return [[]] (one valid “empty” combination)

3. Explore examples.

1. Example 1

Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]

1. Example 2

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

1. Example 3

Input: candidates = [2], target = 1
Output: []

4. Brainstorm 2 - 3 solutions, naive solution first and optimize later. Explain the key idea of each solution.

4.1. Solution 1: Naive Backtracking (DFS) - Time O(k^N), Space O(k)

• At each step:

  • Choose a number

  • Subtract it from target

  • Recurse again with the same index (allow reuse)

• Stop when:

  • target == 0 → valid combination

  • target < 0 → invalid path

• Time: O(k^N)

• Space: O(k)

4.2. Solution 2: Optimized Backtracking with Sorting & Pruning when sum > remaining - Time O(k^N), Space O(k)

• Optimization:

  • If candidates[i] > remaining, break the loop

  • Avoid unnecessary recursion

• Time: O(k^N)

• Space: O(k)

4.3. Solution 3: Dynamic Programming (Advanced)

• Idea:

  • Use DP where dp[t] contains all combinations that sum to t.

  • This is more complex to implement and memory-heavy, so backtracking is preferred in interviews.

• Time: O(T)

• Space: O(T)

5. Implement solutions.

5.1. Backtracking - Time O(2^K), Space O(K)

class Solution:
    def combinationSum(self, nums: List[int], target: int) -> List[List[int]]:
        res = []

        def dfs(i, cur, total):
            if total == target:
                res.append(cur.copy())
                return
            if i >= len(nums) or total > target:
                return

            # Pick nums[i]
            cur.append(nums[i])
            dfs(i, cur, total + nums[i])
            cur.pop()

            # Skip nums[i]
            dfs(i + 1, cur, total)

        dfs(0, [], 0)
        return res

• Time: O(2^K)

• Space: O(K)

• Idea:

Start at i=0 (2)
├── pick 2 → [2]
│   ├── pick 2 → [2,2]
│   │   ├── pick 2 → [2,2,2] ✅
│   │   └── skip 2 → try 3
│   └── skip 2 → try 3
└── skip 2 → try 3

5.2. Backtracking with Prunning - Time O(2^k), Space O(k), k < K by prunning

class Solution:
    def combinationSum(self, nums: List[int], target: int) -> List[List[int]]:
        res = []
        nums.sort()

        def dfs(i, cur, total):
            if total == target:
                res.append(cur.copy())
                return

            for j in range(i, len(nums)):
                if total + nums[j] > target:
                    return
                cur.append(nums[j])
                dfs(j, cur, total + nums[j])
                cur.pop()

        dfs(0, [], 0)
        return res

• Time: O(2^k)

• Space: O(k)

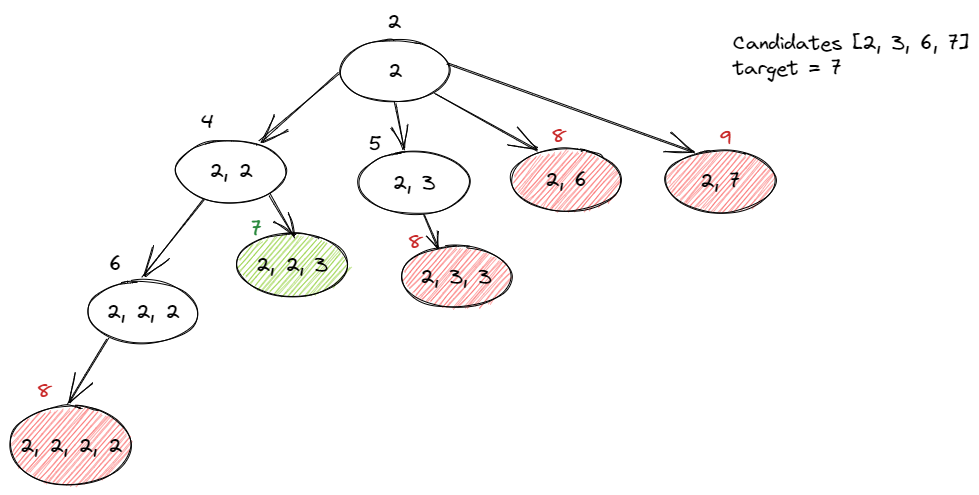
Note: (2,2), (2,3), (2,6), (2,7) => (2,3,3), (2,3,6), (2,3,7), prevent to duplicate value (2,3,2) and (2,2,3)

6. Dry run testcases.