Dynamic Programming, Stack, Merge Intervals
1. Dynamic Programming
1.1. Maximum Earnings From Taxi
from bisect import bisect_right
class Solution:
def maxTaxiEarnings(self, n: int, rides: List[List[int]]) -> int:
# Sort by end time
rides.sort(key=lambda x:x[1])
m = len(rides)
# Create a dp to track maximum until the i
end_times = [ride[1] for ride in rides]
dp = [0] * (m + 1)
# Go backward
for i in range(1, m + 1):
start, end, tip = rides[i - 1]
earning = end - start + tip
# only find in array
idx = bisect_right(end_times, start, lo = 0, hi = i - 1)
dp[i] = max(dp[i - 1], dp[idx] + earning)
return dp[m]
1.2. Partition Equal Subset Sum
- Notes:
For example: arr = [1,2,5]
dp[0] = True -> If we choose [] dp[1] = True -> If we choose [1]
class Solution:
def canPartition(self, nums: List[int]) -> bool:
# Check we can contribute the target // 2 in the current array => If an array can sum to target // 2 in the index i => the rest still target // 2 too
if sum(nums) % 2 != 0:
return False
target = sum(nums) // 2
# dp[i] means "Can we form a subset of numbers from the list that sums up to exactly i?"
dp = [False] * (target + 1)
dp[0] = True # No choice subset is 0, we choose []
# For example, dp[1] = True if we choose [1]
# For each num, we try to add it to existing possible sums.
for num in nums:
for i in range(target, num - 1, -1):
dp[i] = dp[i] or dp[i - num]
return dp[target]
1.3. Subset Sum Problem
arr = [7, 3, 2, 5, 8] target = 14
=> Output [7, 2, 5], True
def isSubsetSum(arr, target_sum):
# dp[i][targetSum] to track whether from i element we can form target
n = len(arr)
dp = [[False] * (target_sum + 1) for _ in range(n + 1)]
# We always can get sum 0 by not choosing anything []
for i in range(n + 1):
dp[i][0] = True
# Backward
for i in range(n + 1):
for j in range(1, target_sum + 1):
if arr[i - 1] > j:
# Can not choose arr[i - 1]
dp[i][j] = dp[i - 1][j]
else:
# Can choose or not
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - arr[i - 1]]
# Unil n -> find target_sum
return dp[n][target_sum]
def printBackward(dp, arr, n, target_sum):
subset = []
i, j = n, target_sum
while i > 0 and j > 0:
if dp[i][j] == dp[i - 1][j]:
i -= 1
else:
subset.append(arr[i - 1])
j -= arr[i - 1]
i -= 1
print(subset[::-1])
def isSubsetSum(arr, target_sum):
# dp[i][targetSum] to track whether from i element we can form target
n = len(arr)
dp = [[False] * (target_sum + 1) for _ in range(n + 1)]
# We always can get sum 0 by not choosing anything []
for i in range(n + 1):
dp[i][0] = True
# Backward
for i in range(n + 1):
for j in range(1, target_sum + 1):
if arr[i - 1] > j:
# Can not choose arr[i - 1]
dp[i][j] = dp[i - 1][j]
else:
# Can choose or not
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - arr[i - 1]]
# Unil n -> find target_sum
result = dp[n][target_sum]
printBackward(dp, arr, n, target_sum)
return result
def printBackward(dp, arr, n, target_sum):
subset = []
i, j = n, target_sum
while i > 0 and j > 0:
if dp[i][j] == dp[i - 1][j]:
i -= 1
else:
subset.append(arr[i - 1])
j -= arr[i - 1]
i -= 1
print(subset[::-1])
print(isSubsetSum([7, 3, 2, 5, 8], 14))
1.4. Knapstack Problem
W = 4, profit[] = [1, 2, 3], weight[] = [4, 5, 1]
Using dp[i][weight] -> Get weight until ith element
def knapsack(weights, values, capacity):
# Create 2-D dp array to carry i item with capacity
n = len(values)
dp = [[0] * (capacity + 1) for _ in range(n + 1)]
# Loop and update array
for i in range(1, n + 1):
for j in range(capacity + 1):
if weights[i - 1] > j:
dp[i][j] = dp[i - 1][j]
else:
# Lay hoac khong lay item i
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weights[i - 1]] + values[i - 1])
return dp[n][capacity]
weights = [2, 3, 4, 5]
values = [3, 4, 5, 6]
capacity = 5
print(knapsack(weights, values, capacity))
1.5. Target Sum (Positive and Negative)
-
Split to array Negative and Positive, select from this collection to get the sum
-
Trước sau gì cũng duyệt hết nên 1-D được rồi
-
Call from [target_sum, num] thôi.
from typing import List
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
if (sum(nums) + target) % 2 != 0 or abs(target) > sum(nums):
return 0
# Find target_sum is postive, and other is negative
target_sum = (sum(nums) + target) // 2
# Trước sau gì cũng duyệt hết nên 1-D được rồi
# Count the way to choose num -> get the sum
dp = [0] * (target_sum + 1)
dp[0] = 1 # One way to make sum 0 (pick nothing)
for num in nums:
for j in range(target_sum, num - 1, -1):
dp[j] = dp[j] + dp[j - num]
return dp[target_sum]
1.6. Unbounded Knapsack
weights = [2, 3, 4] values = [40, 50, 100] capacity = 8
print(unbounded_knapsack(weights, values, capacity)) # Output: 200
-
Cái kia tính tới phần tử i chứ unbounded thì chỉ cần tính theo weight
-
Cái nào cũng 2 vòng lặp, khác nào trong ngoài thôi.
-
Can get ith item, dp[w - weights[i]] là bỏ cùng 1 cái khối lượng đó (bản chất là bỏ cái cũ) + lấy thêm cái đó.
-
Loop tới n thôi, do cái này không có backward.
def unbounded_knapsack(weights, values, capacity):
n = len(weights)
# Max value you can gain after catch i weights
# Cái kia tính tới phần tử i chứ unbounded thì chỉ cần tính theo weight
dp = [0] * (capacity + 1)
dp[0] = 0
# Go forward
for w in range(1, capacity + 1):
for i in range(n):
# Can get ith item, dp[w - weights[i]] là bỏ cùng 1 cái khối lượng đó (bản chất là bỏ cái cũ) + lấy thêm cái đó
if weights[i] <= w:
dp[w] = max(dp[w], dp[w - weights[i]] + values[i])
return dp[capacity]
weights = [2, 3, 4]
values = [40, 50, 100]
capacity = 8
print(unbounded_knapsack(weights, values, capacity)) # Output: 200
1.7. Minimum Cost to Cut a Stick (Min-max trong đoạn -> Cut cut này auto dynamic programming)
from typing import List
class Solution:
def minCost(self, n: int, cuts: List[int]) -> int:
# Step 1: Add 0 and n to the list of cuts and sort it
cuts = [0] + sorted(cuts) + [n]
m = len(cuts)
# Step 2: Initialize a 2D DP array
dp = [[0] * m for _ in range(m)]
# Step 3: Bottom-up DP - compute min cost for all intervals of increasing length
for length in range(2, m): # interval length
for i in range(m - length): # start of interval
j = i + length # end of interval
dp[i][j] = float('inf')
for k in range(i + 1, j): # possible cut points between i and j
cost = cuts[j] - cuts[i] + dp[i][k] + dp[k][j]
dp[i][j] = min(dp[i][j], cost)
# Step 4: Return the minimum cost to cut the entire stick
return dp[0][m - 1]
1.8. Coin Change
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
n = len(coins)
# Number of way to have amount i
dp = [float('inf')] * (amount + 1)
dp[0] = 0
for w in range(1, amount + 1):
for i in range(n):
if coins[i] <= w:
dp[w] = min(dp[w], dp[w - coins[i]] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
1.8. Coin Change 2 (Dynamic Programming Count Sum)
- Bài count sum thì chạy 2 vòng for. For num bên ngoài, weight bên trong.
class Solution:
def change(self, amount: int, coins: List[int]) -> int:
# Init n of the amount
n = len(coins)
# Count way so init 0
dp = [0] * (amount + 1)
dp[0] = 1 # Do not get any coins
for coin in coins:
for w in range(coin, amount + 1):
dp[w] += dp[w - coin]
return dp[amount]
Fibonacci Pattern
1.9. Jump Game II
from typing import List
class Solution:
def jump(self, nums: List[int]) -> int:
n = len(nums)
# Minimum number to jump to ith
dp = [float('inf')] * n
dp[0] = 0
for i in range(1, n):
for j in range(i):
if j + nums[j] >= i: # Can we jump from j to i?
dp[i] = min(dp[i], dp[j] + 1)
return dp[n - 1]
1.10. Min Cost Climbing Stairs
- dp[i] represents min cost to reach step i
from typing import List
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n = len(cost)
dp = [0] * (n + 1) # dp[i] represents min cost to reach step i
for i in range(2, n + 1):
dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2])
return dp[n]
1.11. House Robber
-
Backward: n + 1.
-
Hiện tại thì n thôi
class Solution:
def rob(self, nums: List[int]) -> int:
n = len(nums)
# Find max -> init 0
# dp is max value the thief can get until the home i
if n == 0:
return 0
if n == 1:
return nums[0]
dp = [0] * n
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2, n):
# dp[i - 1] là skip nhà ith
# dp[i - 2] + nums[i] là lấy nhà i - 2 và i
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
return dp[n - 1]
Notes:
-
Cứ capacity thì capacity + 1.
-
Loop trong array thì n.
Notes:
-
Cái chuỗi liên tục (continuous) thì Sliding Window or Longest substring with K character -> You can pop to shrink the string -> Sliding Window (left to right), cái nào based trên quá khứ được dùng Sliding Window.
-
Bớt element trong chuỗi liên tục -> Palindrome -> Dynamic Programming => Cái gì cần tương lai thì dùng pattern + Dynamic Programming.
1.12. Longest Palindromic Substring
-
s[i..j] is a palindrome if:
-
s[i] == s[j] and
-
dp[i+1][j-1] == True (i.e., the inner substring is a palindrome)
-
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n < 2:
return s
# Create a 2D table to store palindrome truth values
dp = [[False] * n for _ in range(n)]
start = 0 # start index of longest palindrome
max_len = 1 # length of longest palindrome
# All substrings of length 1 are palindromes
for i in range(n):
dp[i][i] = True
# Check all substring lengths from 2 to n
for length in range(2, n + 1): # substring length
for i in range(n - length + 1): # starting index
j = i + length - 1 # ending index
if s[i] == s[j]:
if length == 2 or dp[i + 1][j - 1]:
dp[i][j] = True
if length > max_len:
start = i
max_len = length
return s[start:start + max_len]
- Still O(N^2), but Brute Force need O(N) to check palindrome -> But dynamic programming reuse the previous calculation.
1.13. Longest Substring with K Character
class Solution:
def longest_substring_with_k_distinct(self, str, k):
# Given a string, find the length of the longest substring in it with no more than K distinct characters.
windowStart = 0
maxLength = 0
charFrequency = {} # store the frequence count of character
# in the following loop we'll try to extend the range [windowStart, windowEnd]
for windowEnd in range(0, len(str)):
endChar = str[windowEnd]
charFrequency[endChar] = charFrequency.get(endChar, 0) + 1
# shrink the window until we are left with k distinct characters
# in the charFrequency dictionary
while len(charFrequency) > k:
startChar = str[windowStart]
charFrequency[startChar] -= 1
if charFrequency[startChar] == 0:
del charFrequency[startChar]
windowStart += 1
maxLength = max(maxLength, windowEnd - windowStart + 1)
return maxLength
def longest_substring_k_distinct_dp(s: str, k: int) -> int:
n = len(s)
dp = [[0]*n for _ in range(n)]
max_len = 0
for i in range(n):
freq = {}
for j in range(i, n):
freq[s[j]] = freq.get(s[j], 0) + 1
if len(freq) <= k:
dp[i][j] = j - i + 1
max_len = max(max_len, dp[i][j])
return max_len
1.14. Longest Palindromic Subsequence (Subsequence có thể bỏ được)
-
dp[i][j] => mean that is the maximum size palindrome until [i:j].
-
if s[i] == s[j]: dp[i][j] = 2 + dp[i + 1][j - 1], cộng thêm 2 giá trị đầu cuối vào chuỗi hiện có => vẫn là chuỗi palindrome.
-
else: dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]) => bỏ đầu hoặc cuối
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
# Create a 2D DP array initialized to 0
dp = [[0] * n for _ in range(n)]
# All substrings of length 1 are palindromes of length 1
for i in range(n):
dp[i][i] = 1
# Build the DP table
for length in range(2, n + 1): # Substring lengths from 2 to n
for i in range(n - length + 1):
j = i + length - 1
if s[i] == s[j]:
dp[i][j] = 2 + dp[i + 1][j - 1]
else:
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1])
return dp[0][n - 1]
1.15. Longest Common Substring (Không based quá khứ được, 2 chuỗi khác nhau)
- Không based quá khứ được, 2 chuỗi khác nhau -> Dynamic Programming
def longest_common_substring(s1: str, s2: str) -> int:
n1, n2 = len(s1), len(s2)
dp = [[0] * (n2 + 1) for _ in range(n1 + 1)]
max_len = 0
for i in range(1, n1 + 1):
for j in range(1, n2 + 1):
if s1[i - 1] == s2[j - 1]:
dp[i][j] = 1 + dp[i - 1][j - 1]
max_len = max(max_len, dp[i][j])
return max_len
s1 = "geeksforgeeks"
s2 = "practicewritegeekscourses"
print(longest_common_substring(s1, s2))
1.16. Longest Common Subsequence (có thể bỏ i, hoặc j)
class Solution:
def longestCommonSubsequence(self, s1: str, s2: str) -> int:
m, n = len(s1), len(s2)
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if s1[i - 1] == s2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
return dp[m][n]
2. Stack
Use stack when:
-
Nested structures
-
Undo/rollback
-
Balancing / matching elements (like parentheses)
-
Monotonic order tracking (next greater/smaller)
2.1. Basic Calculator
Example: “-3+2”
- First char is '-', so sign = '+' won’t apply right away.
- It sees '-' as the first actual operator, then reads '3', and processes sign == '-', so it appends -3.
class Solution:
def calculate(self, s: str) -> int:
def helper(chars):
num = 0
sign = '+'
stack = []
while chars:
ch = chars.pop(0)
if ch.isdigit():
num = num * 10 + int(ch)
if ch == '(':
num = helper(chars)
# not digit -> sign or not chars
if ch in '+-*/)' or not chars:
if sign == '+':
stack.append(num)
elif sign == '-':
stack.append(-num)
elif sign == '*':
stack.append(stack.pop() * num)
elif sign == '/':
prev = stack.pop()
stack.append(int(prev / num)) # Truncate toward zero
sign = ch
num = 0
if ch == ')':
break
return sum(stack)
return helper(list(s))
2.2 Design LRU
class Node:
def __init__(self, key: int, value: int):
self.key = key
self.value = value
self.prev = None
self.next = None
class LRUCache:
def __init__(self, capacity: int):
self.capacity = capacity
self.cache = {} # key -> Node
self.head = None # LRU
self.tail = None # MRU
def _remove(self, node: Node):
"""Remove a node from the linked list."""
if node.prev:
node.prev.next = node.next
else:
self.head = node.next # node was head
if node.next:
node.next.prev = node.prev
else:
self.tail = node.prev # node was tail
def _add_to_tail(self, node: Node):
"""Add node to the end (MRU)."""
node.prev = self.tail
node.next = None
if self.tail:
self.tail.next = node
self.tail = node
if not self.head:
self.head = node
def get(self, key: int) -> int:
if key not in self.cache:
return -1
node = self.cache[key]
self._remove(node)
self._add_to_tail(node)
return node.value
def put(self, key: int, value: int) -> None:
if key in self.cache:
node = self.cache[key]
node.value = value
self._remove(node)
self._add_to_tail(node)
else:
if len(self.cache) >= self.capacity:
# Remove LRU node
lru = self.head
self._remove(lru)
del self.cache[lru.key]
new_node = Node(key, value)
self.cache[key] = new_node
self._add_to_tail(new_node)
2.3. Queue using Stacks
class MyQueue:
def __init__(self):
self.in_stack = []
self.out_stack = []
def push(self, x: int) -> None:
self.in_stack.append(x)
def pop(self) -> int:
self.peek() # Ensure out_stack has the current front element
return self.out_stack.pop()
def peek(self) -> int:
if not self.out_stack:
while self.in_stack:
self.out_stack.append(self.in_stack.pop())
return self.out_stack[-1]
def empty(self) -> bool:
return not self.in_stack and not self.out_stack
1.20. Stack using Queues
from collections import deque
class MyStack:
def __init__(self):
self.queue = deque()
def push(self, x: int) -> None:
self.queue.append(x)
# Rotate the queue so the last element becomes the front
for _ in range(len(self.queue) - 1):
self.queue.append(self.queue.popleft())
def pop(self) -> int:
return self.queue.popleft()
def top(self) -> int:
return self.queue[0]
def empty(self) -> bool:
return not self.queue
2.4. Evaluation of Postfix Expression
def evaluate_postfix(expression):
stack = []
tokens = expression.split()
for token in tokens:
if token.isdigit():
stack.append(int(token))
else:
b = stack.pop()
a = stack.pop()
if token == '+':
stack.append(a + b)
elif token == '-':
stack.append(a - b)
elif token == '*':
stack.append(a * b)
elif token == '/':
stack.append(int(a / b)) # Integer division
return stack[0]
# Example usage
expr = "5 1 2 + 4 * + 3 -"
print(evaluate_postfix(expr)) # Output: 14
2.5. Evaluation of Prefix Expression
def evaluate_prefix(expression):
stack = []
tokens = expression.split()[::-1] # reverse for right-to-left
for token in tokens:
if token.isdigit():
stack.append(int(token))
else:
a = stack.pop()
b = stack.pop()
if token == '+':
stack.append(a + b)
elif token == '-':
stack.append(a - b)
elif token == '*':
stack.append(a * b)
elif token == '/':
stack.append(int(a / b)) # integer division
return stack[0]
# Example usage
expr = "+ 9 * 2 3"
print(evaluate_prefix(expr)) # Output: 15
2.6. Min Stack
class MinStack:
def __init__(self):
self.stack = [] # Main stack
self.min_stack = [] # Stack to track current min at each level
def push(self, val: int) -> None:
self.stack.append(val)
# Push the new min (either val or current min)
if not self.min_stack or val <= self.min_stack[-1]:
self.min_stack.append(val)
else:
self.min_stack.append(self.min_stack[-1])
def pop(self) -> None:
self.stack.pop()
self.min_stack.pop()
def top(self) -> int:
return self.stack[-1]
def getMin(self) -> int:
return self.min_stack[-1]
2.7. Max Stack
class MaxStack:
def __init__(self):
self.stack = []
self.max_stack = []
def push(self, val: int) -> None:
self.stack.append(val)
if not self.max_stack or val >= self.max_stack[-1]:
self.max_stack.append(val)
else:
self.max_stack.append(self.max_stack[-1])
def pop(self) -> int:
self.max_stack.pop()
return self.stack.pop()
def top(self) -> int:
return self.stack[-1]
def getMax(self) -> int:
return self.max_stack[-1]
def empty(self) -> bool:
return not self.stack
2.8. Decode String
Notes: curr_str = prev_str + curr_str * prev_num
elif char == "]":
prev_num = stack.pop()
prev_str = stack.pop()
# Note
curr_str = prev_str + curr_str * prev_num
class Solution:
def decodeString(self, s: str) -> str:
stack = []
curr_num = 0
curr_str = ""
for char in s:
if char.isdigit():
curr_num = curr_num * 10 + (int(char))
elif char == "[":
stack.append(curr_str)
stack.append(curr_num)
curr_num = 0
curr_str = ""
elif char == "]":
prev_num = stack.pop()
prev_str = stack.pop()
# Note
curr_str = prev_str + curr_str * prev_num
# Case char is character
else:
curr_str += char
return curr_str
2.9. Car Fleet
class Solution:
def carFleet(self, target: int, position: List[int], speed: List[int]) -> int:
# Zip and sort by position
cars = sorted(zip(position, speed), reverse=True)
# The car closest to target is process first, and other cars will pass it
times = [(target - pos) / spd for pos, spd in cars]
# Count fleets
fleets = 0
curr_time = 0
for time in times:
if time > curr_time:
fleets += 1
curr_time = max(curr_time, time)
return fleets
2.10. Generate Parentheses
- Add “(“ to the string as much as possible, and after add “(“, we add “)”
class Solution:
def generateParenthesis(self, n: int) -> List[str]:
res = []
def backtrack(curr_str, open_count, close_count):
if len(curr_str) == 2 * n:
res.append(curr_str)
return
if open_count < n:
backtrack(curr_str + "(", open_count + 1, close_count)
if close_count < open_count:
backtrack(curr_str + ")", open_count, close_count + 1)
backtrack("", 0, 0)
return res
2.11. Longest Valid Parentheses
- Store last “(“ of the character.
class Solution:
def longestValidParentheses(self, s: str) -> int:
max_len = 0
# Magic here to trick case ()
# Store last index of '('
stack = [-1]
for i, char in enumerate(s):
if char == '(':
stack.append(i)
else:
stack.pop()
if stack:
max_len = max(max_len, i - stack[-1])
else:
stack.append(i)
return max_len
2.12. Next Greater Element
Notes: Loop from left to right, if nums[i] > the last stack => Update the index of greater than last stack is nums[i]
def nextGreaterElement(nums):
n = len(nums)
result = [-1] * n
stack = []
for i in range(n):
while stack and nums[i] > nums[stack[-1]]:
idx = stack.pop()
result[idx] = nums[i]
stack.append(i)
return result
2.12. Next Smaller Element
Notes: Loop from left to right, if nums[i] < the last stack => Update the index of greater than last stack is nums[i]
def nextSmallerElement(nums):
n = len(nums)
result = [-1] * n
stack = []
for i in range(n):
while stack and nums[i] < nums[stack[-1]]:
idx = stack.pop()
result[idx] = nums[i]
stack.append(i)
return result
2.13. Daily Temperatures
class Solution:
def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
n = len(temperatures)
stack = []
result = [0] * n
for i in range(n):
while stack and temperatures[i] > temperatures[stack[-1]]:
top = stack.pop()
result[top] = i - top
stack.append(i)
return result
2.14. Largest Rectangle in Histogram
-
Find the first element smaller than the current row => Area.
-
Find the max area from the left and the right too.
-
Compare in both left and right max
Specical case: [2,4,6]
class Solution:
def largestRectangleArea(self, heights: List[int]) -> int:
stack = []
max_area = 0
i = 0
n = len(heights)
while i < n:
if not stack or heights[i] >= heights[stack[-1]]:
stack.append(i)
i += 1
else:
top = stack.pop()
right = i - 1
left = stack[-1] if stack else -1
area = heights[top] * (right - left)
max_area = max(max_area, area)
# Second pass: clean up remaining elements in stack
# Make sure the stack is increment (2,4,6)
while stack:
top = stack.pop()
right = n - 1
left = stack[-1] if stack else -1
area = heights[top] * (right - left)
max_area = max(max_area, area)
return max_area
3. Binary Search
3.1. Koko Eating Bananas
import math
class Solution:
def minEatingSpeed(self, piles: List[int], h: int) -> int:
# Greedy in range [1, max(piles)]
left, right = 1, max(piles)
def canEat(speed):
count = 0
for banana in piles:
count += math.ceil(banana / speed)
return count <= h
while left <= right:
mid = (left + right) // 2
if canEat(mid):
right = mid - 1
else:
left = mid + 1
return left
3.2. Search in Rotated Sorted Array
-
Search the target in array using O(logN)
-
Idea: Using Binary Search of Binary Search
Input: nums = [4,5,6,7,0,1,2], target = 0
Output: 4
Input: nums = [4,5,6,7,0,1,2], target = 3
Output: -1
class Solution:
def search(self, nums: List[int], target: int) -> int:
if not nums:
return -1
left, right = 0, len(nums) - 1
while left <= right:
mid = (left + right) // 2
if nums[mid] == target:
return mid
if nums[left] <= nums[mid]:
if nums[left] <= target < nums[mid]:
right = mid - 1
else:
left = mid + 1
else:
if nums[mid] < target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1
4. Merge Interval (Sort theo start time)
4.1. Check Overlap Interval (Can Attend Meeting)
class Solution:
def canAttendMeetings(self, intervals: List[List[int]]):
# Sort by start time
intervals.sort(key=lambda x:x[0])
n = len(intervals)
# Check validate
for i in range(1, n):
# Overlap
if intervals[i][0] < intervals[i - 1][1]:
return False
return True
4.2. Merge Interval
- Sort by start time:
- If the start < last merge (overlap) => merge to the last.
- Else: append to the list.
def mergeIntervals(intervals):
sortedIntervals = sorted(intervals, key=lambda x: x[0])
merged = []
for interval in sortedIntervals:
if not merged or interval[0] > merged[-1][1]:
merged.append(interval)
else:
merged[-1][1] = max(interval[1], merged[-1][1])
return merged
4.3. Non-Overlapping
- Sort by end => check the overlap with end
def nonOverlappingIntervals(intervals):
if not intervals:
return 0
intervals.sort(key=lambda x: x[1])
end = intervals[0][1]
count = 1
for i in range(1, len(intervals)):
# Non-overlapping interval found
if intervals[i][0] >= end:
end = intervals[i][1]
count += 1
return len(intervals) - count
4.4. Insert Intervals
class Solution:
def insertIntervals(self, intervals: List[List[int]], newInterval: List[int]):
intervals.append(newInterval)
intervals.sort(key=lambda x:x[0])
n = len(intervals)
merged = []
for i in range(0, n):
# Do not overlap
if not merged or intervals[i][0] > merged[-1][1]:
merged.append(intervals[i])
else:
merged[-1][1] = max(merged[-1][1], intervals[i][1])
return merged
4.5. Non-overlap Intervals
- intervals = [[1,3], [2,4], [3,5]]
=> Can not compare intervals[i][0] >= intervals[i - 1][1] => because if we skip the interval[i - 1], it will miss to select the interval[i].
class Solution:
def nonOverlappingIntervals(self, intervals: List[List[int]]):
if not intervals:
return 0
# Sort by end time
intervals.sort(key=lambda x:x[1])
# len of intervals
n = len(intervals)
count = 1
end = intervals[0][1]
# Check the non-overlapping range
for i in range(1, n):
# The overlap interval
if intervals[i][0] >= end:
end = intervals[i][1]
count += 1
return n - count
4.6. Employee Free Time
def employeeFreeTime(intervals):
intervals.sort(key=lambda x:x[0])
n = len(intervals)
merged = []
for i in range(n):
# Do not overlap
if not merged or intervals[i][0] > merged[-1][1]:
merged.append(intervals[i])
else:
merged[-1][1] = max(merged[-1][1], intervals[i][1])
result = []
for i in range(len(merged) - 1):
result.append([merged[i][1], merged[i + 1][0]])
return result
schedule = [[2,4],[7,10],[1,5],[6,9]]
print(employeeFreeTime(schedule))
5. Recursion
-
Rule 1: Luôn có basecase
-
Rule 2: Ví dụ với input nhỏ trước (Lấy ví dụ cái nhỏ nhất trước)
-
Rule 3: Không dùng external varibles, chỉ dùng parameter truyền vào recursive function => làm sao cái parameter đó nó càng gần base case hơn.
-
Rule 4: luôn assump là cái bước trước đó đúng => dùng cái đó chứng minh bước sau
-
Phân biệt Recursion and Tail Recursion:
- Recursion: lưu vào stack call => go the basecase => compute back.
- Tail Recursion: lưu trực tiếp trong hàm recursion => tới bước tail chỉ cần return không cần compute nữa.
6. Backtracking
6.1. Core Idea
- Backtrack is still a tree => depth-first tree searching
function solvable(n):
if n is a leaf node:
if n is a goal node, return true
else return false
else:
for each child c of n:
if solvable(c): return true
return false
How does this work?
- If any child of n is solvable, then n is solvable.
- If no child of n is solvable, then n is not solvable.
boolean solve(Node n):
put node n on the stack
while the stack is not empty:
topnode = the node at the top of the stack
if topnode is a leaf:
If it is a goal node, return true
else pop it off the stack
else:
if topnode has untried children:
push the next untried child onto the stack
else pop the node off the stack
return false
6.2. Prunning
Bản chất check isValid là 1 cách prunning
boolean explore1 (int country, Color color) {
if (country >= map.length())
return goodColoring();
mapColors[country] = color;
for (Color c: Color.values()) {
if (explore1(country + 1, c)) {
return true;
}
}
mapColors[country] = Color.NONE;
return false;
}
- Prunning
boolean explore1 (int country, Color color) {
if (country >= map.length())
return goodColoring();
if (okToColor(country, color)) {
mapColors[country] = color;
for (Color c: Color.values()) {
if (explore1(country + 1, c)) {
return true;
}
}
mapColors[country] = Color.NONE;
}
return false;
}
- Benchmark
Method 1: 2355638070 ns.
Method 2: 20516 ns.
6.3. Binary Search
function solvable(binaryTree):
1. if node is null/None, return false
2. if node is a goal node return true
3. if solvable(node.leftChild), return true
4. if solvable(node.rightChild), return true
5. return false
class Node:
def __init__(self, key):
self.key = key
self.left = None
self.right = None
class BST:
def __init__(self):
self.root = None
# Insert key into BST
def insert(self, key):
self.root = self._insert(self.root, key)
def _insert(self, node, key):
if node is None:
return Node(key)
if key < node.key:
node.left = self._insert(node.left, key)
elif key > node.key:
node.right = self._insert(node.right, key)
return node
# Search for a key
def search(self, key):
return self._search(self.root, key)
def _search(self, node, key):
if node is None or node.key == key:
return node
if key < node.key:
return self._search(node.left, key)
return self._search(node.right, key)
# In-order traversal (sorted order)
def inorder(self):
result = []
self._inorder(self.root, result)
return result
def _inorder(self, node, result):
if node:
self._inorder(node.left, result)
result.append(node.key)
self._inorder(node.right, result)
6.3. Binary Search II
- How to get the solution
def solve(node):
"""Find goal node and report path."""
if node == None:
return None
if node.is_goal_node:
return [node.name]
temp = solve(node.left_child)
if temp != None:
return [node.name] + temp
temp = solve(node.right_child)
if temp != None:
return [node.name] + temp
return None
6.4. Concepts
- Concepts for tree (k-tree)
To search from a node:
if the node is a goal node,
return success.
for each child of the node:
if searching from that child succeeds,
return success.
return failure.
- Concepts for graph
To search from a node:
if the node is a goal node,
return success.
if we've been at this node before,
return failure.
for each neighbor of the node:
if searching from that neighbor succeeds,
return success.
return failure
6.5. Debug:
-
Print the order of function call.
-
Order of sample call
Entering solvable(Root)
| Entering solvable(A)
| | Entering solvable(C)
| | | Entering solvable(null)
| | | solvable(null) returns false
| | | Entering solvable(null)
| | | solvable(null) returns false
| | solvable(C) returns false
| | Entering solvable(D)
| | | Entering solvable(null)
| | | solvable(null) returns false
| | | Entering solvable(null)
| | | solvable(null) returns false
| | solvable(D) returns false
| solvable(A) returns false
| Entering solvable(B)
| | Entering solvable(E)
| | solvable(E) returns true
| solvable(B) returns true
solvable(Root) returns true
- Scan all the path:
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# Build the tree
root = TreeNode(5)
root.left = TreeNode(4)
root.right = TreeNode(8)
root.left.left = TreeNode(11)
root.left.left.left = TreeNode(7)
root.left.left.right = TreeNode(2)
root.right.left = TreeNode(13)
root.right.right = TreeNode(4)
# 5
# / \
# 4 8
# / / \
# 11 13 4
# / \
# 7 2
def findAllPaths(root, target):
res = []
def backtrack(node, path, total):
if not node:
return
path.append(node.val)
total += node.val
print(f"Visited Node: {node.val}, Path: {path}, Sum: {total}")
if not node.left and not node.right and total == target:
print(f"✅ Found valid path: {path}")
res.append(list(path))
backtrack(node.left, path, total)
backtrack(node.right, path, total)
print(f"Backtracking from: {node.val}, Path before pop: {path}")
path.pop()
backtrack(root, [], 0)
return res
paths = findAllPaths(root, 22)
print("All paths that sum to 22:", paths)
Output:
Visited Node: 5, Path: [5], Sum: 5
Visited Node: 4, Path: [5, 4], Sum: 9
Visited Node: 11, Path: [5, 4, 11], Sum: 20
Visited Node: 7, Path: [5, 4, 11, 7], Sum: 27
Backtracking from: 7, Path before pop: [5, 4, 11, 7]
Visited Node: 2, Path: [5, 4, 11, 2], Sum: 22
✅ Found valid path: [5, 4, 11, 2]
Backtracking from: 2, Path before pop: [5, 4, 11, 2]
Backtracking from: 11, Path before pop: [5, 4, 11]
Backtracking from: 4, Path before pop: [5, 4]
Visited Node: 8, Path: [5, 8], Sum: 13
Visited Node: 13, Path: [5, 8, 13], Sum: 26
Backtracking from: 13, Path before pop: [5, 8, 13]
Visited Node: 4, Path: [5, 8, 4], Sum: 17
Backtracking from: 4, Path before pop: [5, 8, 4]
Backtracking from: 8, Path before pop: [5, 8]
Backtracking from: 5, Path before pop: [5]
All paths that sum to 22: [[5, 4, 11, 2]]
- Scan to find 1 path:
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# Build the tree
root = TreeNode(5)
root.left = TreeNode(4)
root.right = TreeNode(8)
root.left.left = TreeNode(11)
root.left.left.left = TreeNode(7)
root.left.left.right = TreeNode(2)
root.right.left = TreeNode(13)
root.right.right = TreeNode(4)
def findOnePath(root, target):
result = []
def backtrack(node, path, total):
if not node:
return False
path.append(node.val)
total += node.val
print(f"Visited Node: {node.val}, Path: {path}, Sum: {total}")
if not node.left and not node.right and total == target:
print(f"✅ Found valid path: {path}")
result.extend(path)
return True
if backtrack(node.left, path, total) or backtrack(node.right, path, total):
return True
print(f"Backtracking from: {node.val}, Path before pop: {path}")
path.pop()
return False
found = backtrack(root, [], 0)
return result if found else None
# ✅ ACTUALLY CALL THE FUNCTION HERE
result = findOnePath(root, 22)
print("Final result:", result)
Output:
Visited Node: 5, Path: [5], Sum: 5
Visited Node: 4, Path: [5, 4], Sum: 9
Visited Node: 11, Path: [5, 4, 11], Sum: 20
Visited Node: 7, Path: [5, 4, 11, 7], Sum: 27
Backtracking from: 7, Path before pop: [5, 4, 11, 7]
Visited Node: 2, Path: [5, 4, 11, 2], Sum: 22
✅ Found valid path: [5, 4, 11, 2]
Final result: [5, 4, 11, 2]
6.6. Word Search
-
Step 1: Base case
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
Backtracking = DFS + Backtrack
class Solution:
def exist(self, board: List[List[str]], word: str) -> bool:
row, col = len(board), len(board[0])
visited = set()
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def backtrack(r, c, index):
# Base case
if index == len(word):
return True
# Prunning
if r < 0 or r >= row or c < 0 or c >= col:
return False
if (r, c) in visited:
return False
if board[r][c] != word[index]:
return False
# Node
visited.add((r, c))
index += 1
# Neighbor
for dr, dc in directions:
nr = r + dr
nc = c + dc
if backtrack(nr, nc, index):
return True
visited.remove((r, c))
index -= 1
return False
for i in range(row):
for j in range(col):
if board[i][j] == word[0]:
visited.clear() # Reset after change 'B'
if backtrack(i, j, 0):
return True
return False
6.7. Letter Combinations of a Phone (Đủ ký tự => Chỉ thêm path tại base case)
- Subsets = Tree + DFS + Backtrack
class Solution:
def letterCombinations(self, digits: str) -> List[str]:
# Subsets = Tree + DFS + Backtrack
phone = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz"
}
result = []
def backtrack(index, path):
# Base case
if index == len(digits):
if path:
result.append(''.join(path[:]))
return
# Prunning
for char in phone[digits[index]]:
# Node
path.append(char)
# Neighbor
backtrack(index + 1, path)
path.pop()
backtrack(0, [])
return result
6.8. Subsets (Không đủ ký tự => tăng index nhưng không thêm path)
- Vẫn index + 1 => nhưng không include in path.
class Solution:
def subsets(self, nums: List[int]):
result = []
def backtrack(index, path):
# Base case
if index == len(nums):
result.append(path[:])
return
# Prunning
# Node
path.append(nums[index])
# Neighbor
backtrack(index + 1, path)
# Backtrack
path.pop()
# Magic here
backtrack(index + 1, path)
backtrack(0, [])
return result
6.9. Generate Parentheses
-
Step 1: Backtrack
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbors
-
Step 5: Backtrack
class Solution:
def generateParenthesis(self, n: int):
result = []
def backtrack(path, open_bracket, close_bracket):
# Base case
if open_bracket == n and close_bracket == n:
result.append(''.join(path[:]))
return
# Prunning
# Node
if open_bracket < n:
path.append('(')
backtrack(path, open_bracket + 1, close_bracket)
path.pop()
# Neighbors
if close_bracket < open_bracket:
path.append(')')
backtrack(path, open_bracket, close_bracket + 1)
path.pop()
backtrack([], 0, 0)
return result
6.10. Combination Sum
- For duplicate same num => For selection in a list => combination in loop, not outside.
class Solution:
def combinationSum(self, candidates: List[int], target: int) -> List[List[int]]:
result = []
def backtrack(index, path, currSum):
# Base case
if currSum == 0:
result.append(path[:])
return
# Prunning
if index == len(candidates) or currSum < 0:
return
# Neighbor
for i in range(index, len(candidates)):
# Node
path.append(candidates[i])
currSum -= candidates[i]
backtrack(i, path, currSum)
# Backtrack
path.pop()
currSum += candidates[i]
backtrack(0, [], target)
return result
7. Tree
7.1. Path Sum:
- Find only 1 path
class Solution:
def pathSum(self, root: TreeNode, target: int) -> bool:
def dfs(node, curr_sum):
if not node:
return False
curr_sum += node.val
# If it's a leaf node, check if the sum matches the target
if not node.left and not node.right:
# Find a function and return
return curr_sum == target
# Continue to left or right subtree
return dfs(node.left, curr_sum) or dfs(node.right, curr_sum)
return dfs(root, 0)
7.2. Count Good Nodes in Binary Tree:
- Cover all
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def goodNodes(self, root: TreeNode) -> int:
# Duyet het
count = 0
def dfs(node, prev_max_value):
nonlocal count
if not node:
return
prev_max_value = max(prev_max_value, node.val)
if node.val == prev_max_value:
count += 1
dfs(node.left, prev_max_value)
dfs(node.right, prev_max_value)
dfs(root, root.val)
return count
7.3. Count Path Sum
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def hasPathSum(self, root: Optional[TreeNode], targetSum: int) -> bool:
if not root:
return False
def dfs(node, total):
if not node:
# In case [1,2] => When traversal right 1 -> null, targetSum = 1 => Count true, we do not allow it.
return False
# Calculate sum until val
total += node.val
# Only check when find in a leaf node
if not node.left and not node.right:
return total == targetSum
left = dfs(node.left, total)
right = dfs(node.right, total)
# Return when found the result
return left or right
return dfs(root, 0)
7.4. Validate BST:
class Solution:
def validateBST(self, root):
def dfs(node, min_val, max_val):
if not node:
return True
if not (min_val < node.val < max_val):
return False
return dfs(node.left, min_val, node.val) and dfs(node.right, node.val, max_val)
return dfs(root, float('-inf'), float('inf'))
7.5. Calculate Tilt
-
Condition 1: Góc nhìn của node.
-
Condition 2: Góc nhìn đối với parent của node.
class Solution:
def calculateTilt(self, root):
# Scan all the tree
tilt = 0
def dfs(node):
nonlocal tilt
if not node:
return 0
# If I a node of the tree, I would return
# Top-down
left = dfs(node.left)
right = dfs(node.right)
tilt += abs(left - right)
# return the sum of the current subtree
# Bottom up
return left + right + node.val
dfs(root)
return tilt
7.6. Path Sum
class Solution:
def pathSum(self, nodes: TreeNode, target: int):
def dfs(node, total):
if not node:
return total == target
# Calculate node
total += node.val
# Prunning here
if not node.left and not node.right and total == target:
return True
left = dfs(node.left, total)
right = dfs(node.right, total)
# Left Right trả gì cho root
return left or right
return dfs(nodes, 0)
7.7. Count Good Nodes in Binary Tree
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def goodNodes(self, root: TreeNode) -> int:
count = 0
def dfs(node, prev_max):
nonlocal count
if not node:
return False
# What node do
if node.val >= prev_max:
prev_max = node.val
count += 1
# What left right do for root
left = dfs(node.left, prev_max)
right = dfs(node.right, prev_max)
return left and right
dfs(root, root.val)
return count
7.8. Validate Binary Search Tree
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def isValidBST(self, root: Optional[TreeNode]) -> bool:
def dfs(node):
if not node:
return True
# Step 1: Prunning
if node.val < node.left or node.val > node.right:
return False
# Step 2: What node do
# Continue to traversal to left and right
# Step 3: What left and right do for node
left = dfs(node.left)
right = dfs(node.right)
return left and right
return dfs(root)
7.9. Binary Tree Tilt
- Step 1: Basecase
- Step 2: Prunning
- Step 3: What node.val do
- Step 4: What left right do for node
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def findTilt(self, root: Optional[TreeNode]) -> int:
titl = 0
def dfs(node):
nonlocal titl
# Step 1: Basecase
if not node:
return 0
# Step 2: Prunning
# Step 3: What node.val do
# Calculate the left and right abs
left = dfs(node.left)
right = dfs(node.right)
titl += abs(left - right)
# Step 4: What left right do for node
return left + right + node.val
dfs(root)
return titl
7.10. Diameter of a Binary Tree
- Height is call from the leaf to the node.
class Solution:
def maxDiameter(self, nodes: TreeNode):
diameterLen = 0
# Height from the leaf to the node
def dfs(node):
nonlocal diameterLen
# Step 1: Base case
if not node:
return 0
# Step 2: Prunning
# No prunning
# Step 3: What node val do
# Find the max distance from its left and right
left = dfs(node.left)
right = dfs(node.right)
# (Root -> right) + (Root -> left)
diameterLen = max(diameterLen, left + right)
# Step 4: Do left and right
# Return the height of current subtree
return 1 + max(left, right)
dfs(nodes)
return diameterLen
7.11. Path Sum II
-
Backtrack.
-
Basecase > Prunning > What Node do > What left and right do.
class Solution:
def pathSum(self, root, target):
res = []
def dfs(node, path, curr_sum):
nonlocal res
# Base case
if not node:
return False
# What node do
path.append(node.val)
curr_sum += node.val
if not node.left and not node.right and curr_sum == target:
res.append(path[:])
# Prunning
if curr_sum > target:
return False
# What left and right do
left = dfs(node.left, path, curr_sum)
right = dfs(node.right, path, curr_sum)
# backtrack
path.pop()
return left and right
dfs(root, [], 0)
return res
7.12. Longest Univalue Path (Hay)
- Step 1: Basecase
- Step 2: Prunning
- Step 3: What node.val do
-
Step 4: What left right do for node
- Assump we already have the largest of the same value in left right
subLeft = dfs(node.left)
subRight = dfs(node.right)
currLeft, currRight = 0, 0
if node.left and node.left.val == node.val:
currLeft = subLeft + 1
if node.right and node.right.val == node.val:
currRight = subRight + 1
max_height = max(max_height, currLeft + currRight)
# What left and right do
return max(currLeft, currRight)
class Solution:
def longestUnivaluePath(self, root: TreeNode):
max_height = 0
# Height from the leaf to curr_node
def dfs(node):
nonlocal max_height
# Base case
if not node:
return 0
# Prunning
# No prunning
# What node do
# The max of same value from left and from right
subLeft = dfs(node.left)
subRight = dfs(node.right)
currLeft, currRight = 0, 0
if node.left and node.left.val == node.val:
currLeft = subLeft + 1
if node.right and node.right.val == node.val:
currRight = subRight + 1
max_height = max(max_height, currLeft + currRight)
# What left and right do
return max(currLeft, currRight)
dfs(root)
return max_height
8. Graph
8.1. Adjacency List
-
Step 1: Basecase
-
Step 2: Visit node
-
Step 3: Visit neighbors
adjList = {
"1": ["2", "4"],
"2": ["1", "3"],
"3": ["2", "4"],
"4": ["1", "3", "5"],
"5": ["4"]
}
def dfs(adjList):
visited = set()
def dfs_helper(node):
if node in visited:
return
# Visit node
print("Visit node: ", node)
visited.add(node)
for neighbor in adjList[node]:
dfs_helper(neighbor)
# Ensure the unconnected graph is still cover
for node in adjList:
if node not in visited:
dfs_helper(node)
adjList = {
"1": ["2", "4"],
"2": ["1", "3"],
"3": ["2", "4"],
"4": ["1", "3", "5"],
"5": ["4"]
}
dfs(adjList)
8.2. Copy Graph
from typing import Dict, List
class IntGraphNode:
def __init__(self, value = 0, neighbors = None):
self.value = value
self.neighbors = neighbors if neighbors is not None else []
class Solution:
def copy_graph(self, node: IntGraphNode) -> Dict[int, List[int]]:
def dfs(root):
visited = set()
result = {}
def dfs_helper(node):
if node.value in visited:
return
visited.add(node.value)
result[node.value] = [neighbor.value for neighbor in node.neighbors]
for neighbor in node.neighbors:
dfs_helper(neighbor)
if root:
dfs_helper(root)
return result
return dfs(node)
8.3. Graph Valid Tree
-
Graph connected.
-
But no cycle.
-
Idea: Visit DFS and check we have visited the parent again.
-
Visited đại từ 1 node nào cũng được => nếu tất cả đều connected component thì có thể visited được hết.
-
-
Using defaultdict for init.
-
Allow to visit a dup again, as long as it is not a parent.
from collections import defaultdict
class Solution:
def graph_valid_tree(self, n, edges):
graph = defaultdict(list)
for start, end in edges:
graph[start].append(end)
graph[end].append(start)
visited = set()
def isCycle(node, parent):
visited.add(node)
for neighbor in graph[node]:
# [0,1] and [1,0] is ok
if neighbor == parent:
continue
# Prunning => True xong không Prunning xuống nữa
if neighbor in visited:
return True
if isCycle(neighbor, node):
return True
return False
# Check not cycle & connected
return not isCycle(0, 0) and len(visited) == n
8.4. Matrix DFS
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
def dfs(matrix):
visited = set()
# Cứ tưởng tượng toạ độ trên trục Oxy (0, 0)
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def dfs_helper(r, c):
# Basecase
if (r, c) in visited:
return
# Prunning
if r < 0 or r >= len(matrix) or c < 0 or c >= len(matrix[0]):
return
# Neighbor
visited.add((r, c))
print("Visit:", (r, c))
for dr, dc in directions:
dfs_helper(r + dr, c + dc)
dfs_helper(0, 0)
matrix = [
[0, 1, 0],
[1, 0, 1],
[0, 1, 0]
]
dfs(matrix)
8.5. Flood Fill
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
class Solution:
def flood_fill(self, image, sr, sc, color):
m, n = len(image), len(image[0])
# Visited
visited = set()
# Directions
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def dfs(r, c, prev_color, color):
# Base case
if (r, c) in visited:
return
# Prunning
if r < 0 or r >= m or c < 0 or c >= n:
return
if image[r][c] != prev_color or image[r][c] == color:
return
# Node
image[r][c] = color
# Neighbor
for dr, dc in directions:
dfs(r + dr, c + dc, prev_color, color)
dfs(sr, sc, image[sr][sc], color)
return image
8.6. Number of Islands
-
Step 1: Basecase
-
Step 2: Prunning
-
Step 3: Node
-
Step 4: Neighbor
-
Notes: Logic check (r, c) in visited only match when the dfs call to the (r, c) => So we still need to check the visited outside too.
class Solution:
def number_of_islands(self, grid):
row, col = len(grid), len(grid[0])
visited = set()
# directions
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def dfs(r, c):
# Base case
# (0, 1) is already in visited if it was reached by DFS from another cell.
if (r, c) in visited:
return
# Prunning
if r < 0 or r >= row or c < 0 or c >= col:
return
if grid[r][c] == 0:
return
# Node
visited.add((r, c))
# Neighbor
for dr, dc in directions:
dfs(r + dr, c + dc)
count = 0
for i in range(row):
for j in range(col):
if grid[i][j] == 1 and (i, j) not in visited:
dfs(i, j)
count += 1
return count
8.7. Boundaries in the Matrix (Surrounded Regions)
-
DFS border ‘O’ to make is ‘S’.
-
Change another ‘O’ to ‘X’.
class Solution:
def surrounded_regions(self, grid: List[List[str]]):
if not grid or not grid[0]:
return []
row, col = len(grid), len(grid[0])
visited = set()
# Directions
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def dfs(r, c):
# Base case
if (r, c) in visited:
return
# Prunning
if r < 0 or r >= row or c < 0 or c >= col:
return
if grid[r][c] != 'O':
return
# Node
visited.add((r, c))
grid[r][c] = 'S'
# Check neighbor
for dr, dc in directions:
dfs(r + dr, c + dc)
# Step 1: DFS in col 0 and col - 1
for i in range(row):
if grid[i][0] == 'O':
dfs(i, 0)
if grid[i][col - 1] == 'O':
dfs(i, col - 1)
# Step 2: DFS in row 0 and row - 1
for j in range(col):
if grid[0][j] == 'O':
dfs(0, j)
if grid[row - 1][j] == 'O':
dfs(row - 1, j)
# Step 3: Change another X to O
for i in range(row):
for j in range(col):
if grid[i][j] == 'O':
grid[i][j] = 'X'
elif grid[i][j] == 'S':
grid[i][j] = 'O'
return grid
8.8. Pacific Atlantic Water Flow
- Backtracking from border to check it contains both ocean.
class Solution:
def pacific_atlantic_flow(self, grid: List[List[int]]):
# Water from high to low
# Top - left: Pacific
# Bottom - Right: Atlantic
if not grid or not grid[0]:
return []
# Get row, col
row, col = len(grid), len(grid[0])
# Visited
pacific = set()
atlantic = set()
# directions
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
def dfs(r, c, visited, prev_height):
# Base case
if (r, c) in visited:
return
# Prunning
if r < 0 or r >= row or c < 0 or c >= col:
return
# If the height is larger than the curr_height => this water flow to the ocean
if grid[r][c] < prev_height:
return
# Node
visited.add((r, c))
# Neighbor
for dr, dc in directions:
dfs(r + dr, c + dc, visited, grid[r][c])
# Check in top and bottom row
for j in range(col):
dfs(0, j, pacific, grid[0][j])
dfs(row - 1, j, atlantic, grid[row - 1][j])
# Check in left and right col
for i in range(row):
dfs(i, 0, pacific, grid[i][0])
dfs(i, col - 1, atlantic, grid[i][col - 1])
# Count both in pacific and atlantic
result = []
for i in range(row):
for j in range(col):
if (i, j) in pacific and (i, j) in atlantic:
result.append([i, j])
return result
9. BFS
9.1. Implement BFS:
Ideas:
- Append to queue.
- Popleft
-
Step 1: Base case
-
Step 2: Root
-
Step 3: Neighbors
-
Step 4: Pop start of the queue.
from collections import deque
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
def bfs(root):
# Base case
if not root:
return []
# Root
result = []
queue = deque([root])
# Neighbors
while queue:
# Add the node in start of the queue
start = queue.popleft()
result.append(start.val)
# Add the left and right of start to queue
if start.left:
queue.append(start.left)
if start.right:
queue.append(start.right)
return result
root = TreeNode(1)
root.left = TreeNode(2, TreeNode(4), TreeNode(5))
root.right = TreeNode(3, TreeNode(6))
print(bfs(root))
9.2. Level Order Sum
-
Step 1: Base case
-
Step 2: Root.
-
Step 3: Neighbors.
-
Step 4: Level of the queue.
-
Step 5: Pop start
from collections import deque
class Solution:
def level_order_sum(self, root: TreeNode):
# Base case
if not root:
return []
# Root
queue = deque([root])
result = []
# Neighbors
while queue:
# Level Queue
level_size = len(queue)
curr_sum = 0
for _ in range(level_size):
# Pop Start
start = queue.popleft()
curr_sum += start.val
if start.left:
queue.append(start.left)
if start.right:
queue.append(start.right)
result.append(curr_sum)
return result
9.3. Rightmost Node
-
Step 1: Base case
-
Step 2: Root
-
Step 3: Neighbors
-
Step 4: Level
-
Step 5: Popleft.
from collections import deque
class Solution:
def rightmostNode(self, root: TreeNode):
# Base case
if not root:
return []
# Root
queue = deque([root])
result = []
# Neighbors
while queue:
# Level size
level_size = len(queue)
for i in range(level_size):
# Pop left
start = queue.popleft()
if i == level_size - 1:
result.append(start.val)
if start.left:
queue.append(start.left)
if start.right:
queue.append(start.right)
return result
9.4. Zigzag Level Order
from collections import deque
class Solution:
def zig_zag(self, root: TreeNode):
# Base case
if not root:
return []
# Root
queue = deque([root])
result = []
odd = True
# Neighbors
while queue:
# Level
level_size = len(queue)
curr_list = []
for _ in range(level_size):
# Pop left
start = queue.popleft()
curr_list.append(start.val)
if start.left:
queue.append(start.left)
if start.right:
queue.append(start.right)
if odd:
result.append(curr_list[:])
else:
result.append(curr_list[::-1])
odd = not odd
return result
9.5. Maximum Width of Binary Tree
- Add the index of the node.
from collections import deque
class Solution:
def maxWidth(self, root: TreeNode):
# Base case
if not root:
return 0
# Node
queue = deque([(root, 0)])
max_width = 0
# Neighbor
while queue:
# Level
level_size = len(queue)
_, first_index = queue[0]
last_index = -1
for i in range(level_size):
# Pop left
start, index = queue.popleft()
if i == level_size - 1:
last_index = index
if start.left:
queue.append((start.left, 2 * index))
if start.right:
queue.append((start.right, 2 * index + 1))
max_width = max(max_width, last_index - first_index + 1)
return max_width
9.6. BFS in Adjacency List
-
Step 1: Base case
-
Step 2: Visit node
-
Step 3: Visit neighbors
-
Step 4: Level
-
Step 5: Pop left
from collections import deque
def bfs(adjList, root):
# Base case
# Root
visited = set()
queue = deque([root])
# Neighbors
while queue:
# Popleft
start = queue.popleft()
print("Visited:", start)
visited.add(start)
# Neighbors
for neighbor in adjList[start]:
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
adjList = {
"1": ["2", "4"],
"2": ["1", "3"],
"3": ["2", "4"],
"4": ["1", "3", "5"],
"5": ["4"]
}
bfs(adjList, "1")
9.7. BFS in Matrix
from collections import deque
def bfs(grid, r, c):
# Base case
# Node
visited = set()
queue = deque([(r, c)])
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
# Neighbors
while queue:
# Pop left
start_row, start_col = queue.popleft()
visited.add((start_row, start_col))
print("Visited:", (start_row, start_col))
# Neighbors
for dr, dc in directions:
n_row = start_row + dr
n_col = start_col + dc
# Prunning
if n_row < 0 or n_row >= len(grid) or n_col < 0 or n_col >= len(grid[0]):
continue
if (n_row, n_col) in visited:
continue
queue.append((n_row, n_col))
visited.add((n_row, n_col))
matrix = [
[0, 0, 0],
[0, 1, 1],
[0, 1, 0]
]
bfs(matrix, 0, 0)
9.8. Adjacency List Level-By-Level
from collections import deque
def bfs(adjList, root):
# Base case
# Root
visited = set()
queue = deque(root)
result = []
# Neighbors
while queue:
# Level
level_size = len(queue)
temp = []
for _ in range(level_size):
# Pop left
start = queue.popleft()
visited.add(start)
temp.append(start)
# Neighbors
for neighbor in adjList[start]:
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
result.append(temp)
return result
adjList = {
"1": ["2", "4"],
"2": ["1", "3"],
"3": ["2", "4"],
"4": ["1", "3", "5"],
"5": ["4"]
}
print(bfs(adjList, "1"))
9.9. Matrix Level-By-Level
- queue = deque([(r, c)]): The way to init a tuple
from collections import deque
def bfs(grid, r, c):
# Base case
# Node
visited = set()
# The way to init a tuple
queue = deque([(r, c)])
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
result = []
# Neighbors
while queue:
level_size = len(queue)
temp = []
for _ in range(level_size):
# Pop left
start_row, start_col = queue.popleft()
visited.add((start_row, start_col))
temp.append((start_row, start_col))
# Visited the neighbors
for dr, dc in directions:
n_row = start_row + dr
n_col = start_col + dc
# Prunning
if n_row < 0 or n_row >= len(grid) or n_col < 0 or n_col >= len(grid[0]):
continue
if (n_row, n_col) in visited:
continue
queue.append((n_row, n_col))
visited.add((n_row, n_col))
result.append(temp)
return result
matrix = [
[0, 0, 0],
[0, 1, 1],
[0, 1, 0]
]
print(bfs(matrix, 0, 0))
9.10. Minimum Knight Moves
-
To count the level of the node in BFS, add the length to a node too.
-
level_size is total of of a level, find shortest path is the count of the level.
from collections import deque
class Solution:
def minimum_knight_moves(self, x: int, y: int):
def bfs(start_x, start_y):
# Base case
# Root
visited = set()
queue = deque([(start_x, start_y)])
# Start with (0, 0) in Oxy axis
directions = [(-1, 2), (-2, 1), (-2, -1), (-1, -2), (1, 2), (2, 1), (2, -1), (1, -2)]
steps = 0
# Neighbors
while queue:
level_size = len(queue)
for _ in range(level_size):
# Pop left
x_idx, y_idx = queue.popleft()
visited.add((x_idx, y_idx))
if (x_idx, y_idx) == (x, y):
return steps
# Neighbors
for dr, dc in directions:
nx_idx = x_idx + dr
ny_idx = y_idx + dc
# Prunning
if (nx_idx, ny_idx) in visited:
continue
queue.append((nx_idx, ny_idx))
visited.add((nx_idx, ny_idx))
steps += 1
return -1
return bfs(0, 0)
9.11. Rotting Oranges
-
BFS and change the value Fresh oranges to rottens oranges.
-
If the value is rottens continue to BFS.
-
Find the intitial rottens index first, only change fresh to rotten oranges.
from collections import deque
class Solution:
def rotting_oranges(self, grid: List[List[str]]):
if not grid or not grid[0]:
return -1
row, col = len(grid), len(grid[0])
fresh_oranges = 0
# Node
visited = set()
queue = deque()
times = -1
for i in range(row):
for j in range(col):
if grid[i][j] == 'R':
queue.append((i, j))
visited.add((i, j))
elif grid[i][j] == 'F':
fresh_oranges += 1
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
# Neighbors
while queue:
# Level (Count)
level_size = len(queue)
for _ in range(level_size):
# Pop left
start_row, start_col = queue.popleft()
# Neighbors
for dr, dc in directions:
n_row = start_row + dr
n_col = start_col + dc
# Prunning
if n_row < 0 or n_row >= row or n_col < 0 or n_col >= col:
continue
if (n_row, n_col) in visited:
continue
if grid[n_row][n_col] != 'F':
continue
grid[n_row][n_col] = 'R'
queue.append((n_row, n_col))
visited.add((n_row, n_col))
fresh_oranges -= 1
times += 1
return times if fresh_oranges == 0 else -1
9.12. Bus Routes
-
BFS
-
Count the level to find the shortest path
-
Step 1: Node
-
Step 2: Neighbor
-
Step 3: Level
-
Step 4: Popleft
from collections import defaultdict
from collections import deque
class Solution:
def bus_routes(self, routes: List[List[int]], source: int, target: int):
# Init
graph = defaultdict(list)
for route in routes:
n = len(route)
for i in range(n):
for j in range(n):
if route[i] != route[j] and route[j] not in graph[route[i]]:
graph[route[i]].append(route[j])
# Node
visited = set()
queue = deque([source])
count = 0
# Neighbor
while queue:
# Level
level_size = len(queue)
for _ in range(level_size):
# Pop left
start = queue.popleft()
if start == target:
return count
for neighbor in graph[start]:
# Prunning
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
count += 1
return -1
9.13. 01-Matrix
from collections import deque
from typing import List
class Solution:
def updateMatrix(self, mat: List[List[int]]) -> List[List[int]]:
m, n = len(mat), len(mat[0])
dist = [[-1 for _ in range(n)] for _ in range(m)]
q = deque()
# Step 1: Initialize the queue with all 0s
for i in range(m):
for j in range(n):
if mat[i][j] == 0:
dist[i][j] = 0
q.append((i, j))
# Step 2: BFS from all 0s
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
count = 1
while q:
level_size = len(q)
for _ in range(level_size):
x, y = q.popleft()
for dx, dy in directions:
nx, ny = x + dx, y + dy
if 0 <= nx < m and 0 <= ny < n and dist[nx][ny] == -1:
dist[nx][ny] = count
q.append((nx, ny))
count += 1
return dist
10. Backtracking
11. Divide and Conquer (quick sort, merge sort, pow x n)
11.1. Merge k Sorted Lists
-
Step 1: Base case
-
Step 2: Split Mid
-
Step 3: Merge 2 list
# Definition for singly-linked list.
# class ListNode:
# def __init__(self, val=0, next=None):
# self.val = val
# self.next = next
class Solution:
def mergeKLists(self, lists: List[Optional[ListNode]]) -> Optional[ListNode]:
# Assump we have 50 lists => change it multiple [list1, list2], [list3, list4]
# Merge range
# Merge 2 lists
if not lists:
return None
return self.merge_range(lists, 0, len(lists) - 1)
def merge_range(self, lists, left, right):
# Base case
# Mid
# Merge 2 list
if left == right:
return lists[left]
mid = (left + right) // 2
l1 = self.merge_range(lists, left, mid)
l2 = self.merge_range(lists, mid + 1, right)
return self.merge_two_lists(l1, l2)
def merge_two_lists(self, l1, l2):
dummy = ListNode()
current = dummy
while l1 and l2:
if l1.val < l2.val:
current.next = l1
l1 = l1.next
else:
current.next = l2
l2 = l2.next
current = current.next
current.next = l1 if l1 else l2
return dummy.next
11.2. Merge Sort
def merge_sort(arr):
# Base case: array of 0 or 1 element is already sorted
if len(arr) <= 1:
return arr
# Split the array into two halves
mid = len(arr) // 2
left = merge_sort(arr[:mid])
right = merge_sort(arr[mid:])
# Merge the sorted halves
return merge(left, right)
def merge(left, right):
result = []
i = j = 0
# Merge two sorted arrays
while i < len(left) and j < len(right):
if left[i] <= right[j]:
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
# Append any remaining elements
result.extend(left[i:])
result.extend(right[j:])
return result
11.3. Max Subarray (Sliding Window - Hay):
from typing import List
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
# Initialize current max and global max to the first element
current_sum = max_sum = nums[0]
# Iterate through the rest of the array
for num in nums[1:]:
# Either start new subarray at current num or extend previous one
current_sum = max(num, current_sum + num)
max_sum = max(max_sum, current_sum)
return max_sum
11.4. Quick Sort
-
Using pivot to sort small < pivot < large.
-
Continue to subarray.
-
j đi sau i đi trước
-
Step 1: Find left - right.
-
Step 2: Find partition in subarray.
-
Step 3: Sort Partition.
def quick_sort(arr):
def partition(low, high):
pivot = arr[high]
i = low - 1
for j in range(low, high):
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[i + 1], arr[high] = arr[high], arr[i + 1]
return i + 1
def quicksort_recursive(low, high):
if low < high:
pi = partition(low, high)
quicksort_recursive(low, pi - 1)
quicksort_recursive(pi + 1, high)
quicksort_recursive(0, len(arr) - 1)
return arr
11.5. Implement Quick Sort
-
Step 1: Find pivot.
-
Step 2: Recursive sort for each pivot of subarray (pivot1 of arr1, pivot2 of arr2)
def partition(arr, left, right):
pivot = arr[right]
i = left - 1
for j in range(left, right):
# Swap to after pivot
# j đi sau i đi trước
if arr[j] <= pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
# Swap pivot
arr[i + 1], arr[right] = arr[right], arr[i + 1]
return i + 1
def quick_sort_recursion(arr, left, right):
if left < right:
pivot_index = partition(arr, left, right)
quick_sort_recursion(arr, left, pivot_index - 1)
quick_sort_recursion(arr, pivot_index + 1, right)
def quick_sort(arr):
quick_sort_recursion(arr, 0, len(arr) - 1)
arr = [1, 7, 4, 1, 10, 9, 2]
quick_sort(arr)
print(arr)
11.6. Implement Merge Sort
def merge_two_lists(l1, l2):
result = []
i, j = 0, 0
while i < len(l1) and j < len(l2):
if l1[i] < l2[j]:
result.append(l1[i])
i += 1
else:
result.append(l2[j])
j += 1
result.extend(l1[i:])
result.extend(l2[j:])
return result
def merge_sort_recursive(arr, left, right):
if left == right:
return [arr[left]]
mid = (left + right) // 2
l1 = merge_sort_recursive(arr, left, mid)
l2 = merge_sort_recursive(arr, mid + 1, right)
return merge_two_lists(l1, l2)
def merge_sort(arr):
if not arr:
return []
return merge_sort_recursive(arr, 0, len(arr) - 1)
arr = [1, 7, 4, 1, 10, 9, 2]
print(merge_sort(arr))
11.7. Pow(x, n):
-
Step 1: Base case
-
Step 2: Divide
-
Step 3: Conquer
class Solution:
def myPow(self, x: float, n: int) -> float:
def exponent(base, pow):
# Base case
if pow == 0:
return 1.0
# Divide
half = exponent(base, pow // 2)
# Conquer
if pow % 2 == 0:
return half * half
else:
return half * half * base
if n < 0:
x = 1 / x
n = -n
return exponent(x, n)
12. Dynamic Programming
12.1. Min Cost Climbing Stairs
- To reach the ith => we need cost[i] + come from (i - 1) or (i - 2).
class Solution:
def minCostClimbingStairs(self, cost: List[int]) -> int:
n = len(cost)
if n == 0:
return cost[0]
if n == 1:
return cost[1]
dp = [0] * (n + 1)
dp[0] = cost[0]
dp[1] = cost[1]
for i in range(2, n + 1):
dp[i] = (0 if i == n else cost[i]) + min(dp[i - 1], dp[i - 2])
return dp[n]
12.2. Minimum Path Sum
-
Max value in (i, j) => dp[i][j] = grid[i][j] + min(dp[i - 1][j], dp[i][j - 1])
-
Remember to fill the first row and left column.
class Solution:
def minPathSum(self, grid: List[List[int]]) -> int:
row, col = len(grid), len(grid[0])
dp = [[0] * col for _ in range(row)]
# Init dp
dp[0][0] = grid[0][0]
# We can do it because we start from (0, 0)
# Start first row
for j in range(1, col):
dp[0][j] = grid[0][j] + dp[0][j - 1]
# Start left column
for i in range(1, row):
dp[i][0] = grid[i][0] + dp[i - 1][0]
# Fill in another value
for i in range(1, row):
for j in range(1, col):
dp[i][j] = grid[i][j] + min(dp[i - 1][j], dp[i][j - 1])
return dp[row - 1][col - 1]
12.3. Coin Change.
-
Can choose between dp[x] and dp[x - coin] + 1 => I mean dp[x - coin] + 1 to reach the target coin.
-
If the coin that can not be make => it still forever (‘inf’ + 1 = ‘inf’)
-
Notes: amount + 1 => Because to reach amount
-
Step 1: Loop coin
-
Step 2: Loop target
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
# Step 1: Loop coin
# Step 2: Loop target
dp = [float('inf')] * (amount + 1)
dp[0] = 0 # Base case
# amount + 1 => Because to reach amount
for coin in coins:
for i in range(coin, amount + 1):
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
12.4. Minimum Falling Path Sum (Hay)
-
Start from the row n - 2 to upward
-
Choose the min count until the last row.
-
Choose the min in the start of the matrix
from typing import List
class Solution:
def minFallingPathSum(self, matrix: List[List[int]]) -> int:
n = len(matrix)
# Start from the second-last row and go upward
for row in range(n - 2, -1, -1):
for col in range(n):
# Get values from the next row: directly below, left-diagonal, right-diagonal
down = matrix[row + 1][col]
left = matrix[row + 1][col - 1] if col > 0 else float('inf')
right = matrix[row + 1][col + 1] if col < n - 1 else float('inf')
# Update current cell with min falling path sum
matrix[row][col] += min(down, left, right)
# The answer is the min in the first row
return min(matrix[0])
12.5. Minimum Cost For Tickets (Hay)
from typing import List
class Solution:
def mincostTickets(self, days: List[int], costs: List[int]) -> int:
day_set = set(days)
last_day = days[-1]
dp = [0] * (last_day + 1)
for day in range(1, last_day + 1):
if day not in day_set:
dp[day] = dp[day - 1] # no travel, cost stays the same
else:
dp[day] = min(
dp[max(0, day - 1)] + costs[0], # 1-day ticket
dp[max(0, day - 7)] + costs[1], # 7-day ticket
dp[max(0, day - 30)] + costs[2] # 30-day ticket
)
return dp[last_day]
12.6. 2 Keys Keyboard (Hay nhưng khó)
class Solution:
def minSteps(self, n: int) -> int:
dp = [0] * (n + 1)
# dp[i] = min number of steps to get i 'A's
for i in range(2, n + 1):
dp[i] = i # worst case: all Paste after one Copy All at 1
for j in range(i // 2, 1, -1):
if i % j == 0:
dp[i] = dp[j] + (i // j)
break # we want the largest factor to minimize steps
return dp[n]
12.7. Perfect Squares (Giống bài chia coin)
import math
class Solution:
def numSquares(self, n: int) -> int:
# dp[i] will be the least number of perfect square numbers that sum to i
dp = [float('inf')] * (n + 1)
dp[0] = 0 # base case: 0 is made up of 0 numbers
# Precompute all perfect squares less than or equal to n
squares = [i * i for i in range(1, int(math.sqrt(n)) + 1)]
for square in squares:
for i in range(square, n + 1):
dp[i] = min(dp[i], dp[i - square] + 1)
return dp[n]
12.8. Last Stone Weight II (Each Stone use once)
-
Step 1: Loop by coin.
-
Step 2: Loop back from target
class Solution:
def lastStoneWeightII(self, stones: List[int]) -> int:
total = sum(stones)
target = total // 2
# dp[j] means the maximum sum we can get which is <= j
dp = [0] * (target + 1)
for stone in stones:
for j in range(target, stone - 1, -1):
dp[j] = max(dp[j], dp[j - stone] + stone)
return total - 2 * dp[target]
12.9. Triangle (Giống Minimum Falling Path Sum)
class Solution:
def minimumTotal(self, triangle: List[List[int]]) -> int:
if not triangle:
return 0
# Start from the bottom row
dp = triangle[-1][:] # Copy the last row
# Iterate from the second-to-last row upward
for row in range(len(triangle) - 2, -1, -1):
for col in range(len(triangle[row])):
# Update dp[col] to be the min path sum from this cell
dp[col] = triangle[row][col] + min(dp[col], dp[col + 1])
return dp[0] # Top element will contain the minimum path sum
Notes:
-
Unbounded Knapstack: Go forward because weight = 0 => dp[cap] = max(dp[cap], dp[cap - weight] + value) => if weight = 0 we can reuse
-
Knapstack 0/1: Go backward => dp[cap] = max(dp[cap], dp[cap - weight] + value) => cap - weight != cap => Due to weight start from end will different than 0.
-
Trùng thì forward, Khác thì backward.
-
Step 1: Loop coin.
-
Step 2: Loop target.
12.10. Ones and Zeroes
12.11. Maximal Square
12.12. Coin Change
- Step 1: Init DP
- Step 2: Loop coin
- Step 3: Loop target
Here’s what happens:
dp[1] = min(dp[1], dp[0] + 1) → 1 coin
dp[2] = min(dp[2], dp[1] + 1) → 2 coins
…
dp[5] = min(dp[5], dp[4] + 1) → 5 coins
Each new dp[i] is built on top of the result from dp[i - coin], which may already include the same coin.
class Solution:
def coinChange(self, coins: List[int], amount: int) -> int:
# Step 1: Init DP
dp = [float('inf')] * (amount + 1)
dp[0] = 0
# Step 2: Loop coin
for coin in coins:
# Step 3: Loop target
for i in range(coin, amount + 1):
dp[i] = min(dp[i], dp[i - coin] + 1)
return dp[amount] if dp[amount] != float('inf') else -1
12.13. Maximal Square (Hay nhưng chưa hiểu)
class Solution:
def maximalSquare(self, matrix: List[List[str]]) -> int:
if not matrix:
return 0
rows, cols = len(matrix), len(matrix[0])
# dp[i][j] will represent the size of the largest square ending at (i, j)
dp = [[0] * (cols + 1) for _ in range(rows + 1)]
max_side = 0
for i in range(1, rows + 1):
for j in range(1, cols + 1):
if matrix[i - 1][j - 1] == '1':
dp[i][j] = min(
dp[i - 1][j], # top
dp[i][j - 1], # left
dp[i - 1][j - 1] # top-left
) + 1
max_side = max(max_side, dp[i][j])
return max_side * max_side # return area
12.14. Ones and Zeroes (Hay)
-
Step 1: DP
-
Step 2: Coin
-
Step 3: Target
-
Forward: coin -> n + 1
-
Backward: n -> coin - 1
class Solution:
def findMaxForm(self, strs: List[str], m: int, n: int) -> int:
# Step 1: DP
dp = [[0] * (n + 1) for _ in range(m + 1)]
# Step 2: Coin
for s in strs:
zeros = s.count('0')
ones = s.count('1')
# Step 3: Target
for i in range(m, zeros - 1, -1):
for j in range(n, ones - 1, -1):
dp[i][j] = max(dp[i][j], dp[i - zeros][j - ones] + 1)
return dp[m][n]
Distinct Ways:
12.15. Climbing Stairs
- To go to the step i => go 1 step from step i - 1 or go 2 steps from i - 2
class Solution:
def climbStairs(self, n: int) -> int:
# To go to the step i => go 1 step from step i - 1 or go 2 steps from i - 2
dp = [0] * (n + 1)
dp[0] = 1
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
12.16. Unique Paths (Hay)
-
Find shortest path using bfs.
-
Count number of way using DP.
class Solution:
def uniquePaths(self, m: int, n: int) -> int:
dp = [[1] * n for _ in range(m)]
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
12.17. Number of Dice Rolls With Target Sum (Hay - 2D DP - Note)
-
Step 1: Roll n times.
-
Step 2: Roll with value.
-
Step 3: Dynamic coin
-
Notes: Thường mấy này hơn nhau -1 lần thôi.
class Solution:
def numRollsToTarget(self, n: int, k: int, target: int) -> int:
dp = [[0] * (target + 1) for _ in range(n + 1)]
dp[0][0] = 1
MOD = 10**9 + 7
for i in range(1, n + 1):
for j in range(1, target + 1):
for dice in range(1, k + 1):
if j - dice >= 0:
dp[i][j] = (dp[i][j] + dp[i - 1][j - dice]) % MOD
return dp[n][target]
12.18. Knight Probability in Chessboard
-
if moves_left == 0 => return 1. Because knight is still on the board after k move
-
for m in range(1, k + 1): # 1️⃣ For each move from 1 to k for r in range(n): # 2️⃣ For each row on the board for c in range(n): # 3️⃣ For each column on the board for dr, dc in directions: # 4️⃣ For each possible knight move
class Solution:
def knightProbability(self, n: int, k: int, row: int, column: int) -> float:
directions = [
(2, 1), (1, 2), (-1, 2), (-2, 1),
(-2, -1), (-1, -2), (1, -2), (2, -1)
]
# dp[m][r][c] = probability of being on cell (r, c) after m moves
dp = [[[0] * n for _ in range(n)] for _ in range(k + 1)]
dp[0][row][column] = 1 # Start at (row, column)
for m in range(1, k + 1): # 1️⃣ For each move from 1 to k
for r in range(n): # 2️⃣ For each row on the board
for c in range(n): # 3️⃣ For each column on the board
for dr, dc in directions: # 4️⃣ For each possible knight move
prev_r, prev_c = r - dr, c - dc
if 0 <= prev_r < n and 0 <= prev_c < n:
dp[m][r][c] += dp[m - 1][prev_r][prev_c] / 8
# Sum up all probabilities of being on the board after k moves
total_prob = sum(dp[k][r][c] for r in range(n) for c in range(n))
return total_prob
12.19. Target Sum (Note)
from typing import List
class Solution:
from typing import List
class Solution:
def findTargetSumWays(self, nums: List[int], target: int) -> int:
total = sum(nums)
if (total - target) % 2 != 0 or total < target:
return 0
neg = (total - target) // 2
# Init DP
dp = [0] * (neg + 1)
dp[0] = 1
# Loop coin
for num in nums:
# Select only 1 => backward
for i in range(neg, num - 1, -1):
if i >= num:
dp[i] = dp[i] + dp[i - num]
return dp[neg]
12.20. Combination Sum IV (Note)
-
Number of ways is always plus
-
We change the order of loops based on what the problem considers unique.
-
Coin change: Coin is unique.
-
Combination: Target is unique.
-
-
Notes: Cái gì unique để ngoài
class Solution:
def combinationSum4(self, nums: List[int], target: int) -> int:
dp = [0] * (target + 1)
dp[0] = 1
# Order matters → outer loop over target
for i in range(1, target + 1):
for num in nums:
if i >= num:
dp[i] += dp[i - num]
return dp[target]
12.21. Knight Dialer (DP in graph - Hay)
class Solution:
def knightDialer(self, n: int) -> int:
MOD = 10**9 + 7
# Knight moves from each digit
moves = {
0: [4, 6],
1: [6, 8],
2: [7, 9],
3: [4, 8],
4: [0, 3, 9],
5: [], # 5 is unreachable by knight
6: [0, 1, 7],
7: [2, 6],
8: [1, 3],
9: [2, 4]
}
# dp[i][j]: number of ways to reach digit j at step i
dp = [ [0] * 10 for _ in range(n) ]
# Base case: 1 way to be at any digit at step 0
for digit in range(10):
dp[0][digit] = 1
# Fill dp table
for i in range(1, n):
for digit in range(10):
for nei in moves[digit]:
dp[i][digit] = (dp[i][digit] + dp[i - 1][nei]) % MOD
return sum(dp[n - 1]) % MOD
12.22. Partition Equal Subset Sum
-
Step 1: Loop num
-
Step 2: Loop backward
class Solution:
def canPartition(self, nums: List[int]) -> bool:
# Find dp sum with nums / 2
total = sum(nums)
if total % 2 != 0:
return False
target = total // 2
dp = [0] * (target + 1)
dp[0] = 1
for num in nums:
for i in range(target, num - 1, -1):
dp[i] += dp[i - num]
return dp[target] != 0
2D Matrix:
-
Step 1: Loop row.
-
Step 2: Loop col.
-
Step 3: Loop coin.
12.23. Soup Servings (Hay, giống bài mua vé ticket)
-
2D array
-
Step 1: Loop row.
-
Step 2: Loop col.
-
Step 3: Loop coin.
class Solution:
def soupServings(self, n: int) -> float:
if n >= 5000:
return 1.0
N = (n + 24) // 25
dp = [[0.0 for _ in range(N + 1)] for _ in range(N + 1)]
# Base cases
for i in range(N + 1):
dp[0][i] = 1.0 # A empty first
dp[i][0] = 0.0 # B empty first
dp[0][0] = 0.5 # Both empty at same time
for a in range(1, N + 1):
for b in range(1, N + 1):
dp[a][b] = 0.25 * (
dp[max(0, a - 4)][b] +
dp[max(0, a - 3)][max(0, b - 1)] +
dp[max(0, a - 2)][max(0, b - 2)] +
dp[max(0, a - 1)][max(0, b - 3)]
)
return dp[N][N]
12.24. Domino and Tromino Tiling
-
Step 1: Loop row.
-
Step 2: Loop col.
-
Step 3: Loop coin.
-
Find a rule
- dp[i - 1]: Vertical
- dp[i - 1] + dp[i - 3]: Horizontal + L-shape
class Solution:
def numTilings(self, n: int) -> int:
MOD = 10**9 + 7
if n == 0:
return 1
if n == 1:
return 1
if n == 2:
return 2
dp = [0] * (n + 1)
dp[0] = 1
dp[1] = 1
dp[2] = 2
for i in range(3, n + 1):
# dp[i - 1]: Vertical
# dp[i - 1] + dp[i - 3]: Horizontal + L-shape
dp[i] = (2 * dp[i - 1] + dp[i - 3]) % MOD
return dp[n]
12.25. Unique Paths II (Hay)
class Solution:
def uniquePathsWithObstacles(self, obstacleGrid: List[List[int]]) -> int:
m, n = len(obstacleGrid), len(obstacleGrid[0])
if obstacleGrid[0][0] == 1 or obstacleGrid[m - 1][n - 1] == 1:
return 0
dp = [[0] * n for _ in range(m)]
dp[0][0] = 1
# DP in first row
for i in range(1, n):
if obstacleGrid[0][i] == 0:
dp[0][i] = dp[0][i - 1]
# DP in left column
for i in range(1, m):
if obstacleGrid[i][0] == 0:
dp[i][0] = dp[i - 1][0]
# DP in other grid
for i in range(1, m):
for j in range(1, n):
if obstacleGrid[i][j] == 0:
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
12.26. Number of Longest Increasing Subsequence
-
Using length[i] to keep the largest length.
-
Using count[i] to count the current largest length.
class Solution:
def findNumberOfLIS(self, nums: List[int]) -> int:
n = len(nums)
length = [1] * (n + 1)
count = [1] * (n + 1)
for i in range(n):
for j in range(i):
if nums[j] < nums[i]:
if length[j] + 1 > length[i]:
length[i] = length[j] + 1
count[i] = count[j]
elif length[j] + 1 == length[i]:
count[i] += count[j]
max_len = max(length)
return sum(count[i] for i in range(n) if length[i] == max_len)
12.17. Out of Boundary Paths
- Thứ tự loop tuỳ depend of row.
class Solution:
def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
MOD = 10**9 + 7
dp = [[[0] * (n + 1) for _ in range(m + 1)] for _ in range(maxMove + 1)]
directions = [(-1, 0), (1, 0), (0, -1), (0, 1)]
for move in range(1, maxMove + 1):
for i in range(m):
for j in range(n):
for dr, dc in directions:
ni, nj = i + dr, j + dc
if ni < 0 or ni >= m or nj < 0 or nj >= n:
# State
dp[move][i][j] = (dp[move][i][j] + 1) % MOD
else:
dp[move][i][j] = (dp[move][i][j] + dp[move - 1][ni][nj]) % MOD
return dp[maxMove][startRow][startColumn]
- DP in Mid of Merge Intervals
12.18. Minimum Cost Tree From Leaf Values
class Solution:
def mctFromLeafValues(self, arr: List[int]) -> int:
n = len(arr)
dp = [[0] * n for _ in range(n)]
max_leaf = [[0] * n for _ in range(n)]
# Precompute the max_leaf[i][j]
for i in range(n):
max_leaf[i][i] = arr[i]
for j in range(i + 1, n):
max_leaf[i][j] = max(max_leaf[i][j - 1], arr[j])
# Interval DP
for length in range(2, n + 1): # length of subarray
for i in range(n - length + 1):
j = i + length - 1
dp[i][j] = float('inf')
for k in range(i, j):
cost = (dp[i][k] + dp[k + 1][j] +
max_leaf[i][k] * max_leaf[k + 1][j])
dp[i][j] = min(dp[i][j], cost)
return dp[0][n - 1]
12.19. Unique Binary Search Trees
-
For n nodes, choose each number 1 to n as root.
The number of unique BSTs with root i is: dp[i-1] (left subtree) × dp[n-i] (right subtree)
-
Step 1: Node trước.
-
Step 2: Value sau
class Solution:
def numTrees(self, n: int) -> int:
dp = [0] * (n + 1)
dp[0] = 1 # Empty tree
dp[1] = 1 # One node tree
for nodes in range(2, n + 1):
for root in range(1, nodes + 1):
left = root - 1
right = nodes - root
dp[nodes] += dp[left] * dp[right]
return dp[n]
12.20. Minimum Score Triangulation of Polygon
-
Step 1: Find i.
-
Step 2: Find sub range j => (i, j).
-
Step 3: Find maximum in range k
class Solution:
def minScoreTriangulation(self, values: List[int]) -> int:
# Find 2D n x n
n = len(values)
dp = [[0] * n for _ in range(n)]
for length in range(3, n + 1):
for i in range(n - length + 1):
# Sub range (i, j)
j = i + length - 1
dp[i][j] = float('inf')
for k in range(i, j):
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j] + values[i] * values[k] * values[j])
return dp[0][n - 1]
12.21. Guess Number Higher or Lower II
Pattern for merge interval DP.
-
Step 1: Length
-
Step 2: Start
-
Step 3: End
class Solution:
def getMoneyAmount(self, n: int) -> int:
dp = [[0] * (n + 1) for _ in range(n + 1)]
for length in range(2, n + 1): # length of interval
for start in range(1, n - length + 2):
end = start + length - 1
dp[start][end] = float('inf')
for x in range(start, end):
cost = x + max(dp[start][x - 1], dp[x + 1][end])
dp[start][end] = min(dp[start][end], cost)
return dp[1][n]
- DP on Strings
12.22. Longest Common Subsequence
-
dp[i][j] represents the length of LCS of s1[:i] and s2[:j]
-
If match, update dp[i][j].
-
Else: skip i or j
class Solution:
def longestCommonSubsequence(self, s1: str, s2: str) -> int:
m, n = len(s1), len(s2)
# dp[i][j] represents the length of LCS of s1[:i] and s2[:j]
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(1, m + 1):
for j in range(1, n + 1):
if s1[i - 1] == s2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] + 1 # Match
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) # Skip one character
return dp[m][n]
12.23. Palindromic Substrings
class Solution:
def countSubstrings(self, s: str) -> int:
n = len(s)
count = 0
dp = [[False] * n for _ in range(n)]
for end in range(n):
for start in range(end + 1):
if s[start] == s[end]:
# If the substring length is <= 3, it's a palindrome
if end - start <= 2:
dp[start][end] = True
else:
# For longer substrings, check the inner substring
dp[start][end] = dp[start + 1][end - 1]
# Count if it's a palindrome
if dp[start][end]:
count += 1
return count
12.24. Longest Palindromic Subsequence
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
dp = [[0] * n for _ in range(n)]
# Base case: every single letter is a palindrome of length 1
for i in range(n):
dp[i][i] = 1
# Fill in order of increasing substring length
for end in range(n):
for start in range(end - 1, -1, -1): # go backward to ensure dp[start + 1][end - 1] is ready
if s[start] == s[end]:
if end - start == 1:
dp[start][end] = 2
else:
dp[start][end] = 2 + dp[start + 1][end - 1]
else:
dp[start][end] = max(dp[start + 1][end], dp[start][end - 1])
return dp[0][n - 1]
- Notes: Substring khác với Subsequence:
- Substring là từ i quay ngược về trước được (1 cái là loop forward)
- Subsequence là cần backward về sau => có thể bỏ bớt ký tự được (1 cái là loop backward)
12.25. Shortest Common Supersequence (Hay)
class Solution:
def shortestCommonSupersequence(self, str1: str, str2: str) -> str:
m, n = len(str1), len(str2)
# Step 1: Find the LCS
dp = [[""] * (n + 1) for _ in range(m + 1)]
for i in range(m):
for j in range(n):
if str1[i] == str2[j]:
dp[i + 1][j + 1] = dp[i][j] + str1[i]
else:
dp[i + 1][j + 1] = max(dp[i + 1][j], dp[i][j + 1], key=len)
lcs = dp[m][n]
# Step 2: Build the SCS using LCS
res = []
i = j = 0
for c in lcs:
while str1[i] != c:
res.append(str1[i])
i += 1
while str2[j] != c:
res.append(str2[j])
j += 1
res.append(c)
i += 1
j += 1
# Add remaining parts
res.append(str1[i:])
res.append(str2[j:])
return ''.join(res)
12.26. Edit Distance (Hay mà khó)
-
How many operations to convert word1[0..i-1] to an empty string?
-
How many operations to convert an empty string to word2[0..j-1]?
-
dp[i - 1][j] → Delete word1[i - 1]
-
dp[i][j - 1] → Insert word2[j - 1]
-
dp[i - 1][j - 1] → Replace word1[i - 1] with word2[j - 1]
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
m, n = len(word1), len(word2)
# dp[i][j] = min operations to convert word1[0..i-1] to word2[0..j-1]
dp = [[0] * (n + 1) for _ in range(m + 1)]
# Initialize base cases
for i in range(m + 1):
dp[i][0] = i # delete all characters
for j in range(n + 1):
dp[0][j] = j # insert all characters
# Fill DP table
for i in range(1, m + 1):
for j in range(1, n + 1):
if word1[i - 1] == word2[j - 1]:
dp[i][j] = dp[i - 1][j - 1] # no operation needed
else:
dp[i][j] = 1 + min(
dp[i - 1][j], # delete
dp[i][j - 1], # insert
dp[i - 1][j - 1] # replace
)
return dp[m][n]
12.27. Distinct Subsequences (Idea giống Edit Distance)
class Solution:
def numDistinct(self, s: str, t: str) -> int:
m, n = len(s), len(t)
# dp[i][j] = number of distinct subsequences of s[0..i-1] that match t[0..j-1]
dp = [[0] * (n + 1) for _ in range(m + 1)]
# An empty t can always be matched by deleting all characters in s
for i in range(m + 1):
dp[i][0] = 1
# Fill the DP table
for i in range(1, m + 1):
for j in range(1, n + 1):
if s[i - 1] == t[j - 1]:
# Match or skip s[i-1]
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
else:
# Skip s[i-1]
dp[i][j] = dp[i - 1][j]
return dp[m][n]
12.28. Minimum ASCII Delete Sum for Two Strings (Giống Longest Common Subsequence)
- Tìm total - 2 * LCS
class Solution:
def minimumDeleteSum(self, s1: str, s2: str) -> int:
m, n = len(s1), len(s2)
# dp[i][j] = max ASCII sum of common subsequence between s1[0..i-1] and s2[0..j-1]
dp = [[0] * (n + 1) for _ in range(m + 1)]
for i in range(m):
for j in range(n):
if s1[i] == s2[j]:
dp[i + 1][j + 1] = dp[i][j] + ord(s1[i])
else:
dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j])
total = sum(ord(c) for c in s1) + sum(ord(c) for c in s2)
common = dp[m][n]
return total - 2 * common
12.29. Longest Palindromic Substring (Hay)
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
if n == 0:
return ""
dp = [[False] * n for _ in range(n)]
start = 0
max_len = 1
for end in range(n):
for i in range(end + 1):
if s[i] == s[end]:
if end - i <= 2:
dp[i][end] = True
else:
dp[i][end] = dp[i + 1][end - 1]
if dp[i][end] and end - i + 1 > max_len:
start = i
max_len = end - i + 1
return s[start:start + max_len]
Decision Making
12.30. House Robber
class Solution:
def rob(self, nums: List[int]) -> int:
if not nums:
return 0
if len(nums) == 1:
return nums[0]
n = len(nums)
dp = [0] * n
dp[0] = nums[0]
dp[1] = max(nums[0], nums[1])
for i in range(2, n):
# Skip the house[i]
# Or stole the house[i]
dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
return dp[-1]
12.31. Best Time to Buy and Sell Stock (Buy 1 time)
from typing import List
class Solution:
def maxProfit(self, prices: List[int]) -> int:
min_price = float('inf') # Initialize to a very high value
max_profit = 0
for price in prices:
if price < min_price:
min_price = price # Update minimum price
else:
max_profit = max(max_profit, price - min_price) # Potential profit
return max_profit
from typing import List
class Solution:
def maxProfit(self, prices: List[int]) -> int:
n = len(prices)
if n == 0:
return 0
dp0 = 0 # Max profit without stock
dp1 = -prices[0] # Max profit with one stock bought
for i in range(1, n):
dp0 = max(dp0, dp1 + prices[i]) # Sell today or do nothing
dp1 = max(dp1, -prices[i]) # Buy today or do nothing
return dp0
12.32. Best Time to Buy and Sell Stock with Transaction Fee
from typing import List
class Solution:
def maxProfit(self, prices: List[int], fee: int) -> int:
if not prices:
return 0
cash = 0
hold = -prices[0] # Buy on day 0
for price in prices[1:]:
cash = max(cash, hold + price - fee) # Sell
hold = max(hold, cash - price) # Buy
return cash
12.33. Best Time to Buy and Sell Stock with Cooldown
💡 DP State Definitions:
We track 3 states:
-
hold: Max profit on day i if holding a stock.
-
sold: Max profit on day i if just sold a stock (cooldown applies next day).
-
rest: Max profit on day i if in cooldown or doing nothing.
from typing import List
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
n = len(prices)
hold = -prices[0] # Buy on day 0
sold = 0 # Nothing sold yet
rest = 0 # Initial rest state
for price in prices[1:]:
prev_hold = hold
prev_sold = sold
prev_rest = rest
hold = max(prev_hold, prev_rest - price) # Buy
sold = prev_hold + price # Sell
rest = max(prev_rest, prev_sold) # Stay resting or go into cooldown
return max(sold, rest) # Final profit must not be holding
12.34. Best Time to Buy and Sell Stock III
from typing import List
class Solution:
def maxProfit(self, prices: List[int]) -> int:
if not prices:
return 0
buy1 = float('-inf')
sell1 = 0
buy2 = float('-inf')
sell2 = 0
for price in prices:
buy1 = max(buy1, -price)
sell1 = max(sell1, buy1 + price)
buy2 = max(buy2, sell1 - price)
sell2 = max(sell2, buy2 + price)
return sell2
12.35. Best Time to Buy and Sell Stock IV
dp[day][transaction][holding]
-
day = current day
-
transaction = number of completed transactions
-
holding = 0 (no stock), 1 (holding stock)
from typing import List
class Solution:
def maxProfit(self, k: int, prices: List[int]) -> int:
n = len(prices)
if n == 0:
return 0
# Optimization for large k
if k >= n // 2:
return sum(
max(prices[i] - prices[i - 1], 0) for i in range(1, n)
)
# dp[i][t][0 or 1]
dp = [[[0] * 2 for _ in range(k + 1)] for _ in range(n)]
for t in range(k + 1):
dp[0][t][0] = 0
dp[0][t][1] = -prices[0] # if we buy on day 0
for i in range(1, n):
for t in range(1, k + 1):
# Not holding
dp[i][t][0] = max(dp[i-1][t][0], dp[i-1][t][1] + prices[i])
# Holding
dp[i][t][1] = max(dp[i-1][t][1], dp[i-1][t-1][0] - prices[i])
return max(dp[n-1][t][0] for t in range(k + 1)) # max profit without holding
13. Scheduling
13.1. Indegree
edges = [(0, 1), (1, 2), (1, 3), (3, 2), (3, 4)]
n = 5
def in_degrees(edges, n):
in_degrees = [0] * n
for u, v in edges:
in_degrees[v] += 1
return in_degrees
print(in_degrees(edges, n))
13.2. Topo Sort (Kahn’s Algorithm)
Notes: Không phải visited mà indegree[i] = 0
-
Indegrees + BFS
-
Step 1: Build Indegree
-
Step 2: Add indegree = 0 to queue
-
Step 3: Node
-
Step 4: Neighbor - add indegree = 0 to queue
-
Step 5: Popleft
from collections import deque
def topo_sort(adjList, n):
# Build indegrees
in_degrees = [0] * n
for u in adjList:
for v in adjList[u]:
in_degrees[v] += 1
# Add indegrees = 0 to queue
# Node
queue = deque([u for u in range(n) if in_degrees[u] == 0])
# Can visit multiple time => make sure indegrees[i] = 0
# visited = set()
result = []
# Neighbor
while queue:
# Popleft
start = queue.popleft()
result.append(start)
for neighbor in adjList[start]:
in_degrees[neighbor] -= 1
if in_degrees[neighbor] == 0:
queue.append(neighbor)
return result
adjList = {
0: [1, 3],
1: [2],
2: [],
3: [1, 4, 5],
4: [5],
5: []
}
n = 5
print(topo_sort(adjList, n + 1))
13.3. Course Schedule
from collections import defaultdict, deque
class Solution:
def canFinish(self, numCourses: int, prerequisites: List[List[int]]):
# Indegree
in_degrees = [0] * numCourses
# Adjancy List
adj_list = defaultdict(list)
for u, v in prerequisites:
in_degrees[v] += 1
adj_list[u].append(v)
# Node
queue = deque([u for u in range(numCourses) if in_degrees[u] == 0])
result = []
# Neighbor
while queue:
# Popleft
start = queue.popleft()
result.append(start)
for neighbor in adj_list[start]:
in_degrees[neighbor] -= 1
if in_degrees[neighbor] == 0:
queue.append(neighbor)
return len(result) == numCourses
13.4. Course Schedule II
from collections import defaultdict, deque
class Solution:
def findOrder(self, numCourses: int, prerequisites: List[List[int]]):
# Indegree
in_degrees = [0] * numCourses
# Adjancy List
adj_list = defaultdict(list)
for u, v in prerequisites:
in_degrees[u] += 1
adj_list[v].append(u)
# Node
queue = deque([u for u in range(numCourses) if in_degrees[u] == 0])
result = []
# Neighbor
while queue:
# Popleft
start = queue.popleft()
result.append(start)
for neighbor in adj_list[start]:
in_degrees[neighbor] -= 1
if in_degrees[neighbor] == 0:
queue.append(neighbor)
return result if len(result) == numCourses else []
13.5. Dijkstra
-
Dijkstra = BFS + thay deque to heapq + dist[i] to store start -> i
-
dist[neighbor] = dist[start] + weight
-
Step 1: Init heap
-
Step 2: Node
-
Step 3: Neighbor
-
Step 4: Dist
-
Find min distance to start -> i -> j -> end, push when dist[neighbor] = dist[start] + weight
import heapq
from collections import defaultdict
def dijkstra(graph, start):
# Init heap
dist = defaultdict(lambda: float('inf'))
# Node
pq = [(0, start)]
dist[start] = 0
# Neighbor
while pq:
curr_dist, start = heapq.heappop(pq)
# Prunning
if curr_dist > dist[start]:
continue
# Dist
for neighbor, weight in graph[start]:
if dist[neighbor] > dist[start] + weight:
dist[neighbor] = dist[start] + weight
heapq.heappush(pq, (dist[neighbor], neighbor))
return dist
graph = {
'A': [('B', 5), ('C', 1)],
'B': [('A', 5), ('C', 2), ('D', 1)],
'C': [('A', 1), ('B', 2), ('D', 4), ('E', 8)],
'D': [('B', 1), ('C', 4), ('E', 3), ('F', 6)],
'E': [('C', 8), ('D', 3)],
'F': [('D', 6)]
}
start_node = 'A'
distances = dijkstra(graph, start_node)
for node in sorted(distances):
print(f"Distance from {start_node} to {node}: {distances[node]}")
13.6. Single-thread CPU
-
Step 1: Start time at task[0]
-
Step 2: Add to queue.
-
Step 3: Process
import heapq
class Solution:
def getOrder(self, tasks: List[List[int]]) -> List[int]:
# Sort tasks
tasks = [(task[0], task[1], idx) for idx, task in enumerate(tasks)]
tasks.sort(key=lambda x:(x[0]))
running_tasks = []
# Need a curr_time
curr_time = tasks[0][0]
# Index
i = 0
n = len(tasks)
# Result
result = []
while i < n or running_tasks:
# Add to queue
while i < n and tasks[i][0] <= curr_time:
process_time, idx = tasks[i][1], tasks[i][2]
heapq.heappush(running_tasks, (process_time, idx))
i += 1
# Process
if running_tasks:
process_time, idx = heapq.heappop(running_tasks)
curr_time += process_time
result.append(idx)
else:
curr_time = tasks[i][0]
return result
13.7. Max CPU Load
-
Step 1: Sort job.
-
Step 2: Auto load job
-
Step 3: Process job and update curr_load
import heapq
def find_max_cpu_load(jobs):
# Sort jobs
jobs.sort(key=lambda x:x[0])
process_tasks = []
# CPU load
max_cpu_load = 0
curr_cpu_load = 0
for job in jobs:
start, end, load = job
while process_tasks and process_tasks[0][0] <= start:
processed_job = heapq.heappop(process_tasks)
curr_cpu_load -= processed_job[1]
# Append to jobs to queue by start_time
heapq.heappush(process_tasks, (end, load))
# Update max_cpu_load
curr_cpu_load += load
max_cpu_load = max(max_cpu_load, curr_cpu_load)
return max_cpu_load
jobs = [(1, 4, 3), (2, 5, 4), (7, 9, 6)]
print(find_max_cpu_load(jobs))
13.8. Multi-thread CPU
import heapq
from typing import List
class Solution:
def getOrder(self, tasks: List[List[int]], k: int) -> List[int]:
tasks = [(task[0], task[1], idx) for idx, task in enumerate(tasks)]
tasks.sort()
task_heap = [] # (-processing_time, idx, enqueue_time)
running_tasks = [] # (end_time, idx)
res = []
time = 0
i = 0
max_end_time = 0
# Create a priority queue of time events (enqueue times and end times)
event_queue = [(task[0], i) for i, task in enumerate(tasks)]
heapq.heapify(event_queue)
while event_queue or task_heap or running_tasks:
# Get the next event time
if event_queue:
next_time, idx = event_queue[0]
if not running_tasks or (running_tasks[0][0] >= next_time):
time = next_time
# Process all enqueue events at this time
while event_queue and event_queue[0][0] <= time:
_ , task_idx = heapq.heappop(event_queue)
enqueue_time, processing_time, idx = tasks[task_idx]
heapq.heappush(task_heap, (-processing_time, idx, enqueue_time))
i += 1
else:
# Fast-forward to next task end time
time = running_tasks[0][0]
elif running_tasks:
time = running_tasks[0][0]
else:
break
# Remove finished tasks
while running_tasks and running_tasks[0][0] <= time:
heapq.heappop(running_tasks)
# Assign available CPUs
while task_heap and len(running_tasks) < k:
neg_processing_time, idx, enqueue_time = heapq.heappop(task_heap)
processing_time = -neg_processing_time
# Start task at max(current time, enqueue time)
start_time = max(time, enqueue_time)
end_time = start_time + processing_time
heapq.heappush(running_tasks, (end_time, idx))
res.append(idx)
max_end_time = max(max_end_time, end_time)
print("Time", max_end_time)
return res
# Test
tasks = [[1, 2], [2, 4], [3, 2], [4, 1]]
k = 2
sol = Solution()
print(sol.getOrder(tasks, k))
13.9. Task Scheduler
- Add tasks to cooldown queue => Only execute the task when come to time.
import heapq
from collections import Counter, deque
from typing import List
class Solution:
def leastInterval(self, tasks: List[str], n: int) -> int:
# Count the frequency of tasks
freq = Counter(tasks)
# Python's heapq is a min-heap, so we store negative frequencies for max-heap behavior
ready = [-cnt for cnt in freq.values()]
heapq.heapify(ready)
# Queue to manage cooldowns: (ready_time, -task_count)
cooldown = deque()
time = 0
while ready or cooldown:
time += 1
# Release from cooldown if task is ready
if cooldown and cooldown[0][0] == time:
heapq.heappush(ready, cooldown.popleft()[1])
if ready:
cnt = heapq.heappop(ready)
if cnt + 1 < 0:
# Add to cooldown queue with ready time = now + n + 1
cooldown.append((time + n + 1, cnt + 1))
return time
13.10. Task Scheduler II
from typing import List
class Solution:
def taskSchedulerII(self, tasks: List[int], space: int) -> int:
last_day = {} # task -> last executed day
day = 0
for task in tasks:
day += 1
if task in last_day and day - last_day[task] <= space:
# If task was executed too recently, jump forward
day = last_day[task] + space + 1
last_day[task] = day
return day
13.11. Process Tasks Using Servers
from typing import List
import heapq
class Solution:
def assignTasks(self, servers: List[int], tasks: List[int]) -> List[int]:
n = len(servers)
time = 0
result = []
# Min-heap for available servers: (weight, index)
available = [(weight, i) for i, weight in enumerate(servers)]
heapq.heapify(available)
# Min-heap for busy servers: (free_time, weight, index)
busy = []
for i, task_time in enumerate(tasks):
time = max(time, i)
# Release servers that have finished by current time
while busy and busy[0][0] <= time:
free_time, weight, index = heapq.heappop(busy)
heapq.heappush(available, (weight, index))
if available:
weight, index = heapq.heappop(available)
heapq.heappush(busy, (time + task_time, weight, index))
result.append(index)
else:
# No server available now, advance time to earliest free server
free_time, weight, index = heapq.heappop(busy)
time = free_time
heapq.heappush(busy, (time + task_time, weight, index))
result.append(index)
return result
13.12. FCFS - First Come First Serve
-
Cons: High waiting time, such as P2, P3 go after but take shorter time to complete => but need to wait.
-
Step 1: Sort by start time.
-
Step 2: Update time.
-
Step 3: Update schedule.
-
Step 4: Using for.
def fcfs(tasks):
# Task
tasks.sort(key=lambda x:x['arrival_time'])
# Time
time = 0
schedule = []
for task in tasks:
if time < task['arrival_time']:
time = task['arrival_time']
start_time = time
end_time = time + task['burst_time']
schedule.append((task['pid'], start_time, end_time))
time = end_time
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 5},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 1},
]
print(fcfs(tasks))
13.13. SJF - Shortest Job First
-
Prior the shortest job first => Narrow the performance of wait time.
-
Cons: Long starving process
import heapq
def sjf(tasks):
tasks.sort(key=lambda x:x['arrival_time'])
# Base
time = 0
schedule = []
# Add them
i = 0
ready = []
n = len(tasks)
while i < n or ready:
while i < n and tasks[i]['arrival_time'] <= time:
heapq.heappush(ready, (tasks[i]['burst_time'], tasks[i]['arrival_time'], tasks[i]['pid'], tasks[i]))
i += 1
if ready:
_, _, _, task = heapq.heappop(ready)
start_time = time
end_time = start_time + task['burst_time']
schedule.append((task['pid'], start_time, end_time))
time = end_time
else:
time = tasks[i]['arrival_time']
return schedule
# Sample test case
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 8},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 4},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 9},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 5}
]
result = sjf(tasks)
for pid, start, end in result:
print(f"Task {pid}: Start at {start}, End at {end}")
13.14. SRTF - Shortest Remaining Time First
import heapq
def srtf(tasks):
# Preprocess: add 'remaining' field and sort by arrival
tasks = sorted([{**t, 'remaining': t['burst_time']} for t in tasks], key=lambda x: x['arrival_time'])
time = 0
i = 0
n = len(tasks)
ready = [] # (remaining_time, arrival_time, pid, task)
schedule = []
completed = 0
last_pid = None
start_time = None
while completed < n:
# Push all tasks that have arrived into the ready
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready, (task['remaining'], task['arrival_time'], task['pid'], task))
i += 1
if ready:
_, _, pid, task = heapq.heappop(ready)
if pid != last_pid:
# Job cu chua xong
if last_pid is not None:
schedule.append((last_pid, start_time, time))
start_time = time
last_pid = pid
# Execute task for 1 time unit
task['remaining'] -= 1
time += 1
if task['remaining'] > 0:
heapq.heappush(ready, (task['remaining'], task['arrival_time'], task['pid'], task))
else:
completed += 1
schedule.append((pid, start_time, time))
last_pid = None
else:
time += 1
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 8},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 4},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 9},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 5}
]
for pid, start, end in srtf(tasks):
print(f"Task {pid}: Start at {start}, End at {end}")
13.15. Round Robin
from collections import deque
def round_robin(tasks, quantum):
# Add remaining time to each task
tasks = sorted([{**t, 'remaining': t['burst_time']} for t in tasks], key=lambda x: x['arrival_time'])
time = 0
schedule = []
i = 0 # Index for incoming tasks
n = len(tasks)
completed = 0
ready = deque()
while completed < n or ready:
# Enready tasks that have arrived
while i < n and tasks[i]['arrival_time'] <= time:
ready.append(tasks[i])
i += 1
if ready:
task = ready.popleft()
start_time = time
duration = min(quantum, task['remaining'])
time += duration
task['remaining'] -= duration
schedule.append((task['pid'], start_time, time))
# But while that task was executing, new tasks might have arrived
while i < n and tasks[i]['arrival_time'] <= time:
ready.append(tasks[i])
i += 1
# If not finished, push back to ready
if task['remaining'] > 0:
ready.append(task)
else:
completed += 1
else:
# No ready task, jump to the next arrival time
if i < n:
time = tasks[i]['arrival_time']
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 5},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 8},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 6}
]
quantum = 3
result = round_robin(tasks, quantum)
for pid, start, end in result:
print(f"Task {pid}: Start at {start}, End at {end}")
13.16. Priority Scheduling
import heapq
def priority_scheduling(tasks):
# Sort by arrival time first
tasks.sort(key=lambda x: x['arrival_time'])
time = 0
i = 0
n = len(tasks)
schedule = []
ready = []
while i < n or ready:
# Push all tasks that have arrived into the ready queue
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready, (task['priority'], task['arrival_time'], task['pid'], task))
i += 1
if ready:
_, _, _, task = heapq.heappop(ready)
start = time
end = start + task['burst_time']
schedule.append((task['pid'], start, end))
time = end
else:
# If no task is ready, jump to the next arrival
time = tasks[i]['arrival_time']
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 10, 'priority': 3},
{'pid': 'P2', 'arrival_time': 2, 'burst_time': 5, 'priority': 1},
{'pid': 'P3', 'arrival_time': 1, 'burst_time': 8, 'priority': 2},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 6, 'priority': 4}
]
result = priority_scheduling(tasks)
for pid, start, end in result:
print(f"Task {pid}: Start at {start}, End at {end}")
13.17. HRRN - Highest Response Ratio Next
import heapq
from typing import List, Dict, Tuple
def hrrn(tasks: List[Dict]) -> List[Tuple[str, int, int]]:
tasks.sort(key=lambda x: x['arrival_time']) # Sort by arrival time once
time = 0
i = 0
ready = []
schedule = []
while i < len(tasks) or ready:
# Load all available tasks into ready queue
while i < len(tasks) and tasks[i]['arrival_time'] <= time:
ready.append(tasks[i])
i += 1
if ready:
heap = []
for task in ready:
wait = time - task['arrival_time']
response_ratio = (wait + task['burst_time']) / task['burst_time']
# Push with negative response ratio to simulate max-heap
heapq.heappush(heap, (-response_ratio, task['arrival_time'], task['pid'], task))
_, _, _, task = heapq.heappop(heap)
ready.remove(task) # Remove the selected task from ready queue
start = time
end = start + task['burst_time']
schedule.append((task['pid'], start, end))
time = end
else:
time = tasks[i]['arrival_time']
return schedule
13.18. Multiple Queue Scheduling
def multiple_queue(tasks, quantum=2):
# First queue: high priority (RR), Second: low (FCFS)
high = [t for t in tasks if t['priority'] == 1]
low = [t for t in tasks if t['priority'] != 1]
high_schedule = round_robin(high, quantum)
low_schedule = fcfs(low)
return high_schedule + low_schedule
13.19. Multilevel Feedback Queue Scheduling
def mlfq(tasks, queues=3, quantum=2):
from collections import deque
levels = [deque() for _ in range(queues)]
tasks = sorted(tasks, key=lambda x: x['arrival_time'])
i = 0
time = 0
remaining = {t['pid']: t['burst_time'] for t in tasks}
level_map = {t['pid']: 0 for t in tasks}
schedule = []
while i < len(tasks) or any(levels):
while i < len(tasks) and tasks[i]['arrival_time'] <= time:
levels[0].append(tasks[i])
i += 1
for q in range(queues):
if levels[q]:
task = levels[q].popleft()
pid = task['pid']
start = time
run = min(quantum * (2 ** q), remaining[pid])
time += run
remaining[pid] -= run
schedule.append((pid, start, time))
while i < len(tasks) and tasks[i]['arrival_time'] <= time:
levels[0].append(tasks[i])
i += 1
if remaining[pid] > 0:
level_map[pid] = min(q + 1, queues - 1)
levels[level_map[pid]].append(task)
break
else:
time = tasks[i]['arrival_time']
return schedule
13.20. SJF - Shortest Job First (Multiple CPU)
import heapq
from typing import List, Dict, Tuple
def sjf_multi_cpu(tasks: List[Dict], k: int) -> List[Tuple[str, int, int, int]]:
tasks.sort(key=lambda x: x['arrival_time']) # sort by arrival_time
n = len(tasks)
i = 0
time = 0
ready = [] # (burst_time, arrival_time, pid, task)
cpu_heap = [] # (available_time, cpu_id)
schedule = []
# Initialize all CPUs as available at time 0
for cpu_id in range(k):
heapq.heappush(cpu_heap, (0, cpu_id))
while i < n or ready or any(cpu[0] > time for cpu in cpu_heap):
# Add tasks that have arrived by current time
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready, (task['burst_time'], task['arrival_time'], task['pid'], task))
i += 1
# Assign tasks to available CPUs
assigned = False
while ready and cpu_heap and cpu_heap[0][0] <= time:
burst_time, arrival_time, pid, task = heapq.heappop(ready)
cpu_available_time, cpu_id = heapq.heappop(cpu_heap)
start_time = max(time, cpu_available_time)
end_time = start_time + burst_time
schedule.append((pid, start_time, end_time, cpu_id))
heapq.heappush(cpu_heap, (end_time, cpu_id))
assigned = True
if not assigned:
next_arrival = tasks[i]['arrival_time'] if i < n else float('inf')
next_cpu_free = cpu_heap[0][0] if cpu_heap else float('inf')
# Move to the next event (task arrival or CPU becomes free)
time = max(time + 1, min(next_arrival, next_cpu_free))
print("Time", time)
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 4},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 1},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 2},
{'pid': 'P5', 'arrival_time': 4, 'burst_time': 5},
]
schedule = sjf_multi_cpu(tasks, k=3)
for pid, start, end, cpu_id in schedule:
print(f"CPU{cpu_id} runs {pid} from {start} to {end}")
13.21. FCFS Multiple CPU
import heapq
def fcfs_multi_cpu(tasks, cpu_count):
# Sort tasks by arrival time
tasks = sorted(tasks, key=lambda x: x['arrival_time'])
# Min-heap of (available_time, cpu_id)
cpu_heap = [(0, cpu_id) for cpu_id in range(cpu_count)]
heapq.heapify(cpu_heap)
schedule = []
for task in tasks:
arrival = task['arrival_time']
burst = task['burst_time']
pid = task['pid']
# Get the earliest available CPU
available_time, cpu_id = heapq.heappop(cpu_heap)
# The task starts at the max of CPU's available time or its own arrival
start_time = max(available_time, arrival)
end_time = start_time + burst
schedule.append({
'pid': pid,
'cpu': cpu_id,
'start_time': start_time,
'end_time': end_time
})
# Update the CPU's available time
heapq.heappush(cpu_heap, (end_time, cpu_id))
return schedule
# Example
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 5},
{'pid': 'P2', 'arrival_time': 1, 'burst_time': 3},
{'pid': 'P3', 'arrival_time': 2, 'burst_time': 1},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 2},
]
result = fcfs_multi_cpu(tasks, cpu_count=2)
for entry in result:
print(entry)
13.22. Priority Scheduling Multiple CPUs
import heapq
def priority_scheduling_multi_cpu(tasks, cpu_count):
tasks = sorted(tasks, key=lambda x: x['arrival_time'])
i = 0
time = 0
n = len(tasks)
cpu_heap = [(0, cpu_id) for cpu_id in range(cpu_count)]
heapq.heapify(cpu_heap)
ready_queue = []
schedule = []
while i < n or ready_queue:
# Add all tasks that have arrived by current time
while i < n and tasks[i]['arrival_time'] <= time:
task = tasks[i]
heapq.heappush(ready_queue, (task['priority'], task['arrival_time'], task['pid'], task))
i += 1
# Assign ready tasks to available CPUs
assigned = False
while ready_queue and cpu_heap and cpu_heap[0][0] <= time:
cpu_available_time, cpu_id = heapq.heappop(cpu_heap)
_, arrival, pid, task = heapq.heappop(ready_queue)
start_time = max(cpu_available_time, arrival, time)
end_time = start_time + task['burst_time']
schedule.append({
'pid': pid,
'cpu': cpu_id,
'start_time': start_time,
'end_time': end_time
})
heapq.heappush(cpu_heap, (end_time, cpu_id))
assigned = True
# If no task is assigned and no CPU is available yet, move time forward
if not assigned:
next_arrival = tasks[i]['arrival_time'] if i < n else float('inf')
next_cpu_free = cpu_heap[0][0] if cpu_heap else float('inf')
# Move to the next event (task arrival or CPU becomes free)
time = max(time + 1, min(next_arrival, next_cpu_free))
return schedule
tasks = [
{'pid': 'P1', 'arrival_time': 0, 'burst_time': 10, 'priority': 3},
{'pid': 'P2', 'arrival_time': 2, 'burst_time': 5, 'priority': 1},
{'pid': 'P3', 'arrival_time': 1, 'burst_time': 8, 'priority': 2},
{'pid': 'P4', 'arrival_time': 3, 'burst_time': 6, 'priority': 4}
]
result = priority_scheduling_multi_cpu(tasks, cpu_count=2)
for r in result:
print(r)
13.23. Top K Smaller Number
-
Heap: The value of root is smaller, larger than other child node => left > right, or right > left, no matters.
-
Step 1: Init heap
-
Step 2: Loop for number
-
Step 3: If len < k => Heap push.
-
Step 4: If len > 5 => Heap pop push.
import heapq
class Solution:
def kthLargest(self, nums: List[int], k: int):
heap = []
for num in nums:
if len(heap) < k:
heapq.heappush(heap, num)
elif num > heap[0]:
heapq.heappushpop(heap, num)
return heap[0]
13.24. K Closest Points to Origin
-
Using max-heap => we need to remove the farthest element.
-
Smallest Element is almost right => We need to fight the farthest element in the heap and remove it.
-
Step 1: Init heap
-
Step 2: Loop for number
-
Step 3: If len < k => Heap push.
-
Step 4: If len > 5 => Heap pop push.
import heapq
class Solution:
def kClosest(self, points: List[List[int]], k: int):
heap = []
for point in points:
x, y = point
distance = x * x + y * y
if len(heap) < k:
heapq.heappush(heap, (-distance, point))
elif distance < -heap[0][0]:
heapq.heappushpop(heap, (-distance, point))
return [item[1] for item in heap]
Notes:
-
Min -> Max Heap
-
Max -> Min Heap
13.24. Find K Closest Element
import heapq
class Solution:
def kClosest(self, nums: List[int], k: int, target: int):
# Max Heap
heap = []
for num in nums:
distance = abs(target - num)
if len(heap) < k:
heapq.heappush(heap, (-distance, num))
elif distance < -heap[0][0]:
heapq.heappushpop(heap, (-distance, num))
result = [item[1] for item in heap]
result.sort()
return result
13.25. Merge K Sort Lists
from typing import List
import heapq
class Solution:
def mergeKLists(self, lists: List[List[int]]) -> List[int]:
heap = []
for l in lists:
for val in l:
heapq.heappush(heap, val)
result = []
while heap:
result.append(heapq.heappop(heap))
return result
14. Sliding Window
14.1. Fruit into market
-
Step 1: Loop from end
-
Step 2: Counting
-
Step 3: Prunning when reach the length
-
Step 4: Increase start
class Solution:
def totalFruit(self, fruits: List[int]) -> int:
k = 2
# Init start
start = 0
n = len(fruits)
state = {}
max_len = 0
# Counting
for end in range(n):
state[fruits[end]] = state.get(fruits[end], 0) + 1
# Prunning
while len(state) > k:
# Update start
state[fruits[start]] -= 1
if state[fruits[start]] == 0:
del state[fruits[start]]
start += 1
max_len = max(max_len, end - start + 1)
return max_len
14.2. Longest Substring Without Repeating Characters
-
Cái trên là 3 loại khác nhau => này bao nhiêu loại cũng được miễn là k dup
-
Bài toán số lượng
class Solution:
def longestSubstringWithoutRepeat(self, s: str):
k = 1
# Init start
start = 0
state = {}
n = len(s)
max_len = 0
# Loop end
for end in range(n):
# Counting
state[s[end]] = state.get(s[end], 0) + 1
while state[s[end]] > k:
state[s[start]] -= 1
if state[s[start]] == 0:
del state[s[start]]
start += 1
max_len = max(max_len, end - start + 1)
return max_len
14.3. Longest Repeating Character Replacement
-
Step 1: Loop from end
-
Step 2: Counting
-
Step 3: Prunning when reach the length
-
Step 4: Increase start
-
Step 5: Find max_len outside.
class Solution:
def characterReplacement(self, s: str, k: int):
state = {}
start = 0
max_len = 0
max_freq = 0
# Loop end
for end in range(len(s)):
state[s[end]] = state.get(s[end], 0) + 1
max_freq = max(max_freq, state[s[end]])
while (end - start + 1 - max_freq) > k:
state[s[start]] -= 1
if state[s[start]] == 0:
del(state[s[start]])
start += 1
max_len = max(max_len, end - start + 1)
return max_len
14.4. Fixed-Length Sliding Window
-
Step 1: Loop end
-
Step 2: Prunning but end - start + 1 = k
-
Step 3: Increase start.
-
Step 4: Find max_len in prunning.
def max_subarray_sum(nums, k):
start = 0
state = 0
max_sum = 0
# Loop end
for end in range(len(nums)):
state += nums[end]
# Prunning
if end - start + 1 == k:
# Update max_sum
max_sum = max(max_sum, state)
state -= nums[start]
# Increase start
start += 1
return max_sum
nums = [2, 1, 5, 1, 3, 2]
k = 3
print(max_subarray_sum(nums, k))
14.5. Maximum Sum of Subarrays of Size K
-
Step 1: Loop end.
-
Step 2: Prunning when end - start + 1 = k.
-
Step 3: Update max_len trong loop.
class Solution:
def maxSum(self, nums: List[int], k: int):
state = 0
start = 0
max_sum = 0
for end in range(len(nums)):
state += nums[end]
# Prunning
if end - start + 1 == k:
# Update max here
max_sum = max(max_sum, state)
state -= nums[start]
start +=1
return max_sum
14.6. Max Points You Can Obtain From Cards
class Solution:
def maxScore(self, cards, k):
total = sum(cards)
if k >= len(cards):
return total
state = 0
max_points = 0
start = 0
for end in range(len(cards)):
state += cards[end]
if end - start + 1 == len(cards) - k:
max_points = max(total - state, max_points)
state -= cards[start]
start += 1
return max_points
14.7. Max Sum of Distinct Subarrays Length k
-
Step 1: Subarray length k => Find max event in loop when end - start + 1 == k.
-
Step 2: Subarray length k => Handle state count in when end - start + 1 == k.
class Solution:
def maxSum(self, nums: List[int], k: int):
state = {}
curr_sum = 0
start = 0
max_sum = 0
for end in range(len(nums)):
state[nums[end]] = state.get(nums[end], 0) + 1
curr_sum += nums[end]
# Prunning
if end - start + 1 == k:
if len(state) == k:
# Update max here
max_sum = max(max_sum, curr_sum)
curr_sum -= nums[start]
state[nums[start]] -= 1
if state[nums[start]] == 0:
del(state[nums[start]])
start += 1
return max_sum
15. Linked List
15.1. Traversing a Linked List
- Step 1: Using only current
def findLength(head):
length = 0
current = head
while current:
length += 1
current = current.next
return length
15.2. Deleting a Node With a Given Target
-
Step 1: Using current and prev
-
Step 2: Read from prev to curr:
- prev = curr
- curr = curr -> next
def deleteNode(head, target):
if head.val == target:
return head.next
prev = None
curr = head
while curr:
if curr.val == target:
prev.next = curr.next
break
prev = curr
curr = curr.next
return head
15.3. Fast & Slow Pointer
- Step 1: Điều kiện fast & fast.next.next
def fastAndSlow(head):
fast = head
slow = head
while fast && fast.next:
fast = fast.next.next
slow = slow.next
return slow
15.4. Detect Cycle
- Step 1: Điều kiện fast & fast.next.next
class Solution:
def hasCycle(self, head: Optional[ListNode]) -> bool:
slow = head
fast = head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
if slow == fast:
return True
return False
15.5. Reversing a Linked List
-
Step 1: Using prev and current.
-
Step 2: Chỗ này tư duy kiểu gán theo thứ tự => curr->next = prev, thứ tự gán prev = current, current = next.
def reverse(head):
prev = None
current = head
while current:
next_ = current.next
current.next = prev
prev = current
current = next_
return prev
15.3. Merge Two Linked List
-
Step 1: Init head.
-
Step 2: Assign head to head of l1 or head of l2.
-
Step 3: Using tail = head, using tail to transfer the 2 linked list.
def merge_lists(l1, l2):
if not l1: return l2
if not l2: return l1
if l1.val < l2.val:
head = l1
l1 = l1.next
else:
head = l2
l2 = l2.next
tail = head
while l1 and l2:
if l1.val < l2.val:
tail.next = l1
l1 = l1.next
else:
tail.next = l2
l2 = l2.next
tail = tail.next
tail.next = l1 or l2
return head
15.4. Palindrome Linked List
Idea:
-
Step 1: Reverse second half.
-
Step 2: Compare 2 lists.
def is_palindrome(head):
# find middle node of the list
slow = fast = head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
# reverse second half of the list
curr, prev = slow, None
while curr:
next_ = curr.next # save next node
curr.next = prev # reverse pointer
prev = curr # move pointers
curr = next_
# Check palindrome
left, right = head, prev
while right:
if left.val != right.val:
return False
left = left.next
right = right.next
return True
15.5. Remove Nth Node From End of List (Hay)
-
Step 1: Cho con fast đi trước n steps.
-
Step 2: Chạy con fast vs slow cùng tới end.
-
Step 3: Trỏ con slow tới slow.next.next.
def removeNthFromEnd(head, n):
dummy = ListNode(0)
dummy.next = head
fast, slow = dummy, dummy
for _ in range(n):
fast = fast.next
while fast.next:
fast = fast.next
slow = slow.next
# remove nth node from end
slow.next = slow.next.next
return dummy.next
15.6. Reorder List
-
Step 1: Reverse second half of list
-
Step 2: Merge first half with reversed second half
def reorderList(head):
if not head or not head.next:
return head
# find middle node
slow = fast = head
while fast and fast.next:
fast = fast.next.next
slow = slow.next
# reverse second half of list
prev, curr = None, slow
while curr:
next_ = curr.next
curr.next = prev
prev, curr = curr, next_
# merge first and reversed second half of list
first, second = head, prev
while second.next:
first.next, first = second, first.next
second.next, second = first, second.next
return head
15.7. Swap Nodes in Pairs
-
Idea: Reverse pair + next
-
Using con dummyNode, prev, current.
-
Step 1: Dùng prev, current xong thêm vô list mới cũng được.
def swapPairs(head):
dummy = ListNode(0)
dummy.next = head
tail, first = dummy, head
while first and first.next:
second = first.next
# swap nodes
tail.next = second
first.next = second.next
second.next = first
tail = first
first = first.next
return dummy.next
16. Two Pointer
16.1. Two Pointer (2 end)
- Step 1: Same with binary search => but do not use mid = (left + right) / 2
def twoSum(nums, target):
left, right = 0, len(nums) - 1
while left < right:
current_sum = nums[left] + nums[right]
if current_sum == target:
return True
if current_sum < target:
left += 1
else:
right -= 1
return False
16.2. Container With Most Water
- Step 1: Same with binary search => but do not use mid = (left + right) / 2
class Solution:
def max_area(self, heights):
# Left and right but not mid
left, right = 0, len(heights) - 1
max_area = 0
while left < right:
width = right - left
height = min(heights[left], heights[right])
curr_area = width * height
max_area = max(max_area, curr_area)
if heights[left] < heights[right]:
left += 1
else:
right -= 1
return max_area
16.3. Three Sum
- Step 1: Giữ 1 số dầu => xong binary search trong đoạn còn lại => N * O(N) => O(N^2).
16.4. Triangle Numbers
- Step 1: Sort and keep the largest number => Keep it => Find 2 sums.
class Solution:
def triangleNumber(self, nums: List[int]):
nums.sort()
n = len(nums)
count = 0
for end in range(n - 1, -1, -1):
target = nums[end]
left, right = 0, end - 1
while left < right:
curr_sum = nums[left] + nums[right]
if curr_sum > target:
count += right - left # Node here (Keep right)
right -= 1
else:
left += 1
return count
16.5. Move Zeroes
-
Step 1: Init the nextNonZeros => Increase it by condition.
-
Step 2: Go from left to right => If meet 0 => Swap to the back.
class Solution:
def moveZeroes(self, nums: List[int]):
n = len(nums)
nextNonZeros = 0
for i in range(n):
if nums[i] != 0:
nums[i], nums[nextNonZeros] = nums[nextNonZeros], nums[i]
nextNonZeros += 1
return nums
16.6. Remove duplicates
-
Step 1: Init the nextNonDup => Increase it by condition.
-
Step 2: If nums[i] != nums[nextNonDup - 1] => Increase nextNonDup
class Solution:
def removeDuplicates(self, nums: List[int]) -> int:
nextNonDup = 0
n = len(nums)
for i in range(n):
if i == 0 or nums[i] != nums[nextNonDup - 1]:
nums[nextNonDup] = nums[i]
nextNonDup += 1
return nextNonDup
16.7. Sort Flag (Merge 2 cái idea lại)
-
Step 1: nums[i] = 0 -> swap to left
-
Step 2: nums[i] = 1 -> Keep.
-
Step 3: nums[i] = 2 -> Swap right
Chỉ swap left thì i += 1 thôi.
- Notes: Merge 2 cái idea lại => Bản chất duyệt đầu cuối, khác cái Move Zeros do bài đó chỉ có move cuối, còn cái này move 2 đầu nên phải có duyệt đầu cuối.
class Solution:
def sortColors(self, nums: List[int]):
left, right = 0, len(nums) - 1
i = 0
while i <= right:
if nums[i] == 0:
nums[i], nums[left] = nums[left], nums[i]
left += 1
i += 1
elif nums[i] == 1:
i += 1
else:
nums[i], nums[right] = nums[right], nums[i]
right -= 1
return nums
16.8. Trapping Rain Water
Idea:
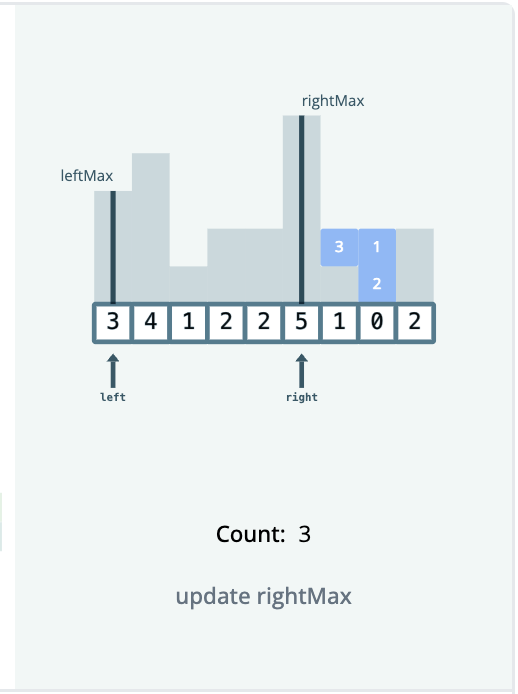
class Solution:
def trappingWater(self, heights: List[int]):
if not heights:
return 0
left, right = 0, len(heights) - 1
leftMax, rightMax = heights[left], heights[right]
count = 0
while left < right:
if rightMax > leftMax:
left += 1
if heights[left] > leftMax:
leftMax = heights[left]
else:
count += leftMax - heights[left]
else:
right -= 1
if heights[right] > rightMax:
rightMax = heights[right]
else:
count += rightMax - heights[right]
return count
17. Dymamic Programming
17.1. Top-down
Top Down = DFS + memo table
-
Step 1: Basecase.
-
Step 2: Prunning.
-
Step 3: Memoization.
-
Step 4: Node.
-
Step 5: Neighbors.
=> Bản chất vẫn đi tìm dp[n].
def climbStairs(n: int) -> int:
memo = {}
def climb_helper(i: int) -> int:
# Base case
if i <= 1:
return 1
# Memoization
if i in memo:
return memo[i]
# Node
memo[i] = climb_helper(i - 1) + climb_helper(i - 2)
return memo[i]
return climb_helper(n)
17.2. Bottom-up
-
Build a table from dp[0] -> dp[n]
-
Step 1: Base case => what is needed for first build.
-
Step 2: Node.
-
Step 3: Condition.
-
Step 4: Neighbors
def stairs(n):
if n <= 1:
return 1
dp = [0] * (n + 1)
dp[0] = 1
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
17.3. Dynamic Programming Problems
- It has optimal substructure (it can be solved using recursion)
- It has overlapping subproblems (the same recursive call is made multiple times)
Idea:
- Top-down first:
-
Step 1: Write base case.
- If we have 0 houses, we can’t collect any treasure, so dp(0) = 0.
- If we have 1 house, we can only collect the treasure from the first house, so dp(1) = treasure[0].
-
Step 2: Write a rob_helper(i).
-
Step 3: Add memoization.
def rob(treasure):
if not treasure:
return 0
def rob_helper(i):
if i == 0:
return 0
if i == 1:
return treasure[0]
skip = rob_helper(i - 1)
take = rob_helper(i - 2) + treasure[i - 1]
return max(skip, take)
return rob_helper(len(treasure))
- Bottom-up DP:
- Covert memoization table to bottom-up DP
def rob(treasure):
if not treasure:
return 0
# initialize dp array
dp = [0] * (len(treasure) + 1)
# fill in base cases (dp[0] = 0 already)
dp[1] = treasure[0]
# iterate to fill in the rest of the array
for i in range(2, len(treasure) + 1):
# fill in dp[i] using the recurrence relation
take = dp[i - 2] + treasure[i - 1]
skip = dp[i - 1]
dp[i] = max(take, skip)
return dp[len(treasure)]
17.4. Rob Treasure Problem
-
Step 1: Init DFS Helper.
-
Step 2: Base case
-
Step 2: Memoization.
-
Step 3: Node
-
Step 4: Result
Because we have N houses => We gain treasure at the (i - 1)th house.
- Top-down:
def rob(treasure):
if not treasure:
return 0
def rob_helper(i):
# Base case
if i == 0:
return 0
if i == 1:
return treasure[0]
# Node
take = rob_helper(i - 2) + treasure[i - 1]
skip = rob_helper(i - 1)
# Result
return max(take, skip)
n = len(treasure)
return rob_helper(n)
treasure = [2, 7, 9, 3, 1]
print(rob(treasure)) # Output: 12
- Memoization:
- Add memo to store the current result => memo = {} => if i in memo => return memo[i] => memo[i] = max(take, skip)
def rob(treasure):
if not treasure:
return 0
memo = {}
def rob_helper(i):
# Base case
if i == 0:
return 0
if i == 1:
return treasure[0]
# Memoization
if i in memo:
return memo[i]
# Node
take = rob_helper(i - 2) + treasure[i - 1]
skip = rob_helper(i - 1)
memo[i] = max(take, skip)
# Result
return memo[i]
n = len(treasure)
return rob_helper(n)
treasure = [2, 7, 9, 3, 1]
print(rob(treasure)) # Output: 12
- Bottom-up:
-
Covert memoization table in top-down to bottom-up.
-
Store data with (n + 1) elements
Step 1: Init dp tables.
Step 2: Base case for start calculate.
Step 3: Calculate.
def rob(treasure):
if not treasure:
return 0
# Init dp table
n = len(treasure)
dp = [0] * (n + 1)
# Base case
dp[0] = 0
dp[1] = treasure[0]
for i in range(2, n + 1):
# Calculate
dp[i] = max(dp[i - 1], dp[i - 2] + treasure[i - 1])
return dp[n]
treasure = [2, 7, 9, 3, 1]
print(rob(treasure)) # Output: 12
17.5. Counting Bits
class Solution:
def count_bits(self, n: int):
dp = [0] * (n + 1)
for i in range(1, n + 1):
dp[i] = dp[i // 2] + (i % 2)
return dp
17.6. Decode Ways
-
Previous 1-bit: d[i] += d[i - 1]
-
Previous 2-bit: d[i] += d[i - 2]
class Solution:
def num_decodings(self, s: str):
if not s or s[0] == '0':
return 0
n = len(s)
dp = [0] * (n + 1)
dp[0], dp[1] = 1, 1
for i in range(2, n + 1):
digit = s[i - 1]
if int(digit) != 0:
dp[i] += dp[i - 1]
digit = s[i - 2:i]
if 10 <= int(digit) <= 26:
dp[i] += dp[i - 2]
return dp[n]
17.7. Maximal Square
class Solution:
def maximal_square(self, matrix: List[List[int]]):
if not matrix:
return 0
r = len(matrix)
c = len(matrix[0])
dp = [[0] * (c + 1) for _ in range(r + 1)]
max_side = 0
for i in range(1, r + 1):
for j in range(1, c + 1):
if matrix[i - 1][j - 1] == 1:
top = dp[i - 1][j]
left = dp[i][j - 1]
diag = dp[i - 1][j - 1]
dp[i][j] = min(top, left, diag) + 1
max_side = max(max_side, dp[i][j])
return max_side * max_side
17.8. Robot Unique Paths
- Idea: Loop in top and left border
class Solution:
def unique_paths(self, m: int, n: int) -> int:
# Initialize a 2D array with dimensions m x n
dp = [[0] * n for _ in range(m)]
# base case: there is only one way to reach any cell in the first row (moving only right)
for i in range(n):
dp[0][i] = 1
# Set base case: there is only one way to reach any cell in the first column (moving only down)
for j in range(m):
dp[j][0] = 1
# Fill the rest of the dp array
for i in range(1, m):
for j in range(1, n):
dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
return dp[m - 1][n - 1]
17.9. Longest Increasing Subsequence
- Idea: dp[i] = max(dp[i], dp[j] + 1)
class Solution:
def longest_increasing_subsequence(self, nums: List[int]):
if not nums:
return 0
n = len(nums)
dp = [1] * n
for i in range(1, n):
for j in range(i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
return max(dp)
17.20. Word Break
class Solution:
def word_break(self, s: str, wordDict: List[str]):
dp = [False] * (len(s) + 1)
dp[0] = True
for i in range(1, len(s) + 1):
for word in wordDict:
if i >= len(word) and dp[i - len(word)]:
sub = s[i - len(word):i]
if sub == word:
dp[i] = True
break
return dp[len(s)]
17.21. Job Scheduling
from bisect import bisect_right
from typing import List
class Solution:
def job_scheduling(self, startTime: List[int], endTime: List[int], profit: List[int]) -> int:
# Sort jobs by end time
jobs = sorted(zip(startTime, endTime, profit), key=lambda x: x[1])
# Extract end times for binary search
ends = [job[1] for job in jobs]
dp = [0] * (len(jobs) + 1)
for i in range(1, len(jobs) + 1):
start, end, p = jobs[i - 1]
idx = bisect_right(ends, start)
dp[i] = max(dp[i - 1], dp[idx] + p)
return dp[-1]
18. Greedy
18.1. Greeds and Cookies
- Using i and j in 2 array, only increase i when pass the condition.
def findContentChildren(greeds, cookies):
greeds.sort()
cookies.sort()
count = 0
i, j = 0, 0
while i < len(greeds) and j < len(cookies):
# current cookie can satisfy current child
if cookies[j] >= greeds[i]:
count += 1
i += 1
j += 1
return count
18.2. Best Time to Buy and Sell Stock
def maxProfit(prices):
if not prices:
return 0
min_price = prices[0]
max_profit = 0
for price in prices:
min_price = min(min_price, price)
max_profit = max(max_profit, price - min_price)
return max_profit
18.3. Gas Station
def canCompleteCircuit(gas, cost):
if sum(gas) < sum(cost):
return -1
start, fuel = 0, 0
for i in range(len(gas)):
if fuel + gas[i] - cost[i] < 0:
# can't reach next station:
# try starting from next station
start, fuel = i + 1, 0
else:
# can reach next station:
# update remaining fuel
fuel += gas[i] - cost[i]
return start
18.4. Jump Game
class Solution:
def canJump(self, nums: List[int]):
max_reach = 0
for i in range(len(nums)):
if i > max_reach:
return False
max_reach = max(max_reach, i + nums[i])
return True
